The Standardized Test season is finally over for us, NYC public school students and parents. I don’t really want to discuss the pros and cons of the standardized tests here, but, rather, show the two math problems from my daughter’s test prep materials that stuck with me. I don’t remember the exact formulation, but they look something like this.
Problem 1 (3rd grade short-answer problem): Mary took the elevator from the 2nd floor 7 floors up and then 4 floors down. What floor is she at? Explain. You may want to draw a diagram to help you think.
The answers are judged on a scale from 1 to 4, 1 means below expectation, 2 – approaches expectation, 3 – meets expectation, and 4 – exceeds expectation. My daughter’s teacher showed me her guidelines – the examples of the students’ answers and the grades they are assigned. Unfortunately, I only remember two out of four, but here they are.
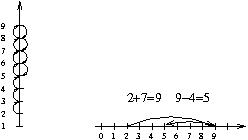
Answer 1 comes with the diagram on the left and says: “First Mary went up so I counted up by one seven times. Then Mary went down so I counted down by one four times. I arrived at 5. Mary is on the 5th floor.” Answer 2 comes with the diagram and “math sentences” on the right and says “Mary is on 5th floor”
One of the answers got the score of 2, and the other the score of 4. Can you guess which? How would you assign the grades? Both results are correct. Both have a diagram. In the first answer, a third grader still counts “by one”. The second does not offer much explanation, even though I would say that the diagram is explanatory enough. The first answer gets a score of 4, the second a score of 2. The high score for the first answer came as a surprise for me. I think that the third grader, who is supposed to know addition/subtraction “number facts”, like 2+7=9 and 9-4=5, should not be praised for counting by one. How does that “exceeds expectation” for a child who had been learning addition for at least three years by the end of the 3rd grade? But what I really think unfair is to assign “approaches expectation” to the second answer. The kid demonstrated mathematical maturity by writing “math sentences” rather than counting by one. The comments from the mathematics experts from the NYC Department of Education give the reason for low score. The student does not explain that addition is used because the elevator goes up, and subtraction because it goes down.
Apparently, this ’addition is used because… and subtraction because…’ key phrases is the main thing those who grade the tests are looking for. Kids are trained to write why they use addition (or subtraction, etc…), and it’s OK, it doesn’t hurt to be able to explain the reasoning. But don’t you think that it is the potential mathematician who is getting punished here, getting discouraged by the low grade? The kid demonstrated perfectly abstract mathematical thinking: so what if an elevator goes vertically, the horizontal number line does the job just as well, things does not have to be taken literally. The number line concept is introduced at the end of the first grade in the Everyday Mathematics series used by many schools, so it’s not that the kid invented it (or, worse, learned in Saturday “cram” school imposed on him or her by tiger parents). Even if he/she did, it is definitely not wrong. “Number facts” are there so that we don’t count by ones (what if there are too many ones to count?) By moving to the right on the number line, the student explained addition, and moving to the left, subtraction. How come it only “approaches expectation”, which means that it is still below expectation? Doesn’t it deserve a 3, at least?
Problem 2 (4th grade multiple choice): Estimate the product of 19 and 24. (a) 500 (b) 450 (c) 400 (d) 300.
My first thought is:19 is almost 20, 24 is almost 25, and it’s easy enough to multiply 20 and 25. So the answer must be 500. My second thought is: hmmm, isn’t the whole point of estimation that there is no single right answer? Different people find different ways to simplify their calculations and estimate things. What kind of tricky question is that? May be they want the number which is the closest to the true product? After all, the closer to the true result, the better estimation is. The product is 456, so the right answer is 450, then? No. The reasoning of the DOE math experts is that 19 rounds to 20, 24 also rounds to 20, so the answer is 400.
Now, may be, since I am not a native English speaker, I don’t really understand the meaning of the word “estimate”, but I am pretty sure it doesn’t mean “round to the nearest tens”. Nevertheless, that is what students are supposed to do. By the rules of rounding, 24 rounds to 20, not 25, all right, I know that. But doesn’t the whole point of estimation get lost here? The Webster’s dictionary says that to estimate is “to judge tentatively or approximately the value…”, to “determine roughly the size…”. In mathematics, to estimate means to find a lower or upper boundary of a quantity that cannot be calculated precisely. That’s not what the test question asks for. Are there other mathematical meanings of “estimate”? If the layperson’s meaning of the word “estimate” is assumed in the question, then what’s wrong with 500, or 450 for the answer?
Of course, children are trained to do what they are supposed to do, that’s what the test prep is for. They know that if they see the word “estimate”, they are supposed to round. But again, the ones who are better mathematicians, who can make more sophisticated calculations in their heads, get punished. And that’s a pity.
۳. استفاده همزمان از اکانت دیگر( حتی Basic ) مجاز نمیباشد و باعث غیرفعال شدن trial میشود. روی گزینه ایمیل کلیک می نمایید و در قسمت اول شما لازم است برای خود یک Username تعریف نمایید ، دقت نمایید بعد از انتخاب username در آینده شما فقط و فقط یکبار می توانید آن را تغییر دهید. در سایت تریدینگ ویو شما ابتدا لاحلیل افراد دیگر نیز استفاده نمایید . 2. بصورت تخصصی در ضمینه خرید اکانت تریدینگ ویو یا سایر سایت های دیگر فعالیت میکنیم. شما می توانید سیگنال بیت کوین، سیگنال اتریوم، سیگنال بایننس کوین، سیگنال تتر و سایر استیبل کوین ها و ارزهای دیجیتال را از طریق خرید سرویس های طلایی و نقره ای سیگنالی تریدینگ دریافت نمایید. از آنجایی که اکانت های Premium یک ماهه هستند و بعد از هر ماه باید یک اکانت پریمیوم دیگر بسازید ، که نیازمند یک ایمیل جدید است ، پیشنهاد
exactly. iam agree with you
thnks sir
Pinoy Lambingan at Orihinal na may Pinoy Tv Replay
Students from less privileged socioeconomic backgrounds may also face challenges.
I hope the writer and the team will be more successful.
Good very useful
thank you
Great post — these examples are distressing! This resonates with discussions I’ve been having lately with pedagogy-minded folk around my office. What are our students meant to think of all this? How the heck are they supposed to develop mathematical intuition, when the rules employed are so arbitrary? In fact, I am trying to imagine what kind of rules I could teach them, that would result in them giving the “correct” answers to your examples — frankly, I have no idea!
Great post — these examples are distressing! This resonates with discussions I’ve been having lately with pedagogy-minded folk around my office. What are our students meant to think of all this? How the heck are they supposed to develop mathematical intuition, when the rules employed are so arbitrary? In fact, I am trying to imagine what kind of rules I could teach them, that would result in them giving the “correct” answers to your examples — frankly, I have no idea!
I really love the Articles more helpful
Nice and Educative!
Professor Ocken,
I have been wondering the same thing as well. Since CUNY educates the majority of NYC high school graduates, it would be natural for the faculty to have some input into what the NYC students learn in school. I am afraid that the answer is NO, but if someone knows otherwise, HOW CAN I GET ON THAT COMMITTEE???
My concern is with the mathematical competence of people who make up the exams.
For example, The June 2011 Algebra 2/Trigonometry Regents exam has at least 2 serious errors.
Problem 32 (long response) says: if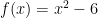
, find 
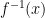. Of course, the given function (without restriction on its domain) has no inverse. The scoring rubric is as follows: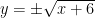
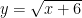
Full credit:
Half credit:
Zero credit is awarded otherwise. In particular, it appears that a response indicating the error in the problem would not be granted any credit.
Problem 8 (multiple choice) asks students to choose the equation represented by the given graph, which does not indicate any scale on either axis. Only by assuming that each box is a unit square can one answer the question. Many student errors in precalculus relate to precisely that assumption. A related misconception is that the only input needed to sketch a graph are integer values of the independent variable.
It would be interesting to find out whether any math professors (from CUNY or elsewhere) were asked to vet the exam.
Stanley Ocken
CCNY Math
Hi there just wanted to give you a quick heads up and let you know a few of the
pictures aren’t loading properly. I’m not sure why but I think its a linking issue.
I’ve tried it in two different browsers and both show the same results.
Jonas,
The most cynical of the answers would be that out students are NOT MEANT to think… Quite a few of the commenters to the posts regarding testing on NYTimes SchoolBook and Insideschools websites (these are the only ones I read) think that there is a government conspiracy not to teach children to think, seriously…
I don’t believe that standardized testing necessarily contradicts teaching kids to think, more that the new generation of teachers don’t know HOW to teach kids to think. I am afraid I don’t, either…
Great post — these examples are distressing! This resonates with discussions I’ve been having lately with pedagogy-minded folk around my office. What are our students meant to think of all this? How the heck are they supposed to develop mathematical intuition, when the rules employed are so arbitrary? In fact, I am trying to imagine what kind of rules I could teach them, that would result in them giving the “correct” answers to your examples — frankly, I have no idea!