Last week when I was trying to sort out a combinatorial question related to my research, I accidentally ended up redoing some fun geometry of the type covered (?) in an undergraduate discrete math, or intro to topology course.
I’m going to ramble on a bit about some fun pictorial counting games, with no particular point in mind, except to show some pretty relations.
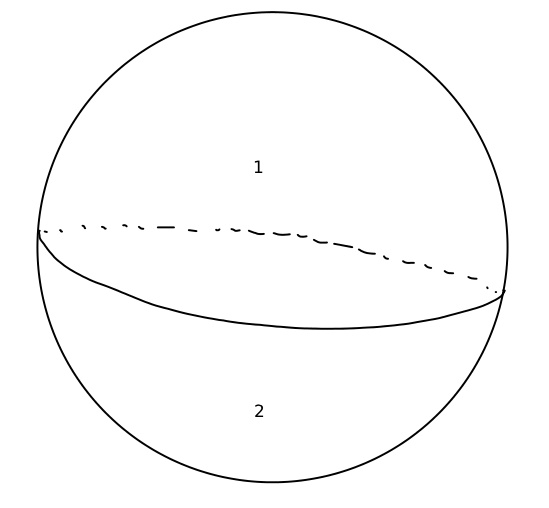
The first has to do with geometrical arrangements on a sphere. It’s not hard to see (unless you are Camille Jordan) that if you draw a circle on a sphere it separates the surface into two regions.
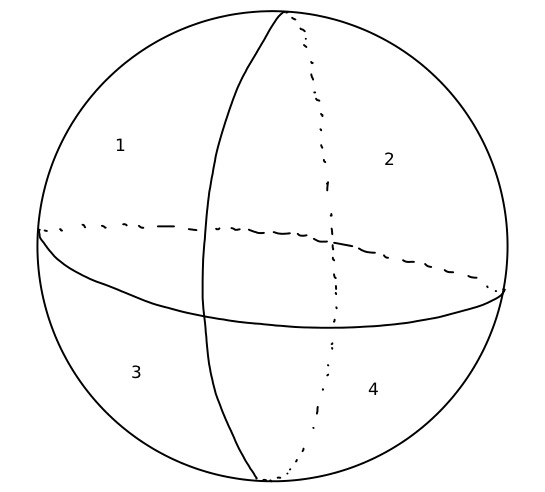
The circle on the sphere in the figure is a special kind of curve called a great circle, which divides the sphere into to equal halves. A great thing about great circles is that any two of them intersect in exactly two points. You can easily see this if we add another line to the picture.
Notice that now the sphere has been split into four. What happens if we add another great circle? The diagram begins to get a little busy.
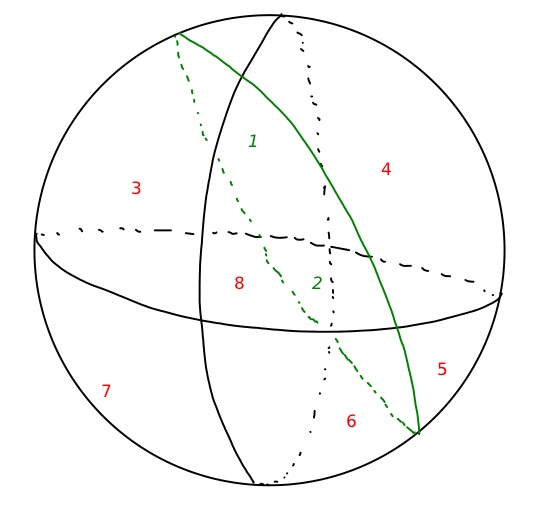
Now a new great circle has been added in green. The red numbers should be “seen” as being on the front of the sphere, whereas the green italicized numbers should be seen as being written on the “inside” of the sphere (to label regions that are mostly on the back).
What we have now is just a somewhat skewed version of the well known fact that three planes with one common point divide space into octants (whereas two lines divide a plane into quadrants).
Notice that up until now, each time we’ve added a new great circle the number of regions has doubled. It might be natural to think that this pattern will continue, and that if we add a fourth line then the sphere will be divided into sixteen regions. Let’s add a new line and see. The diagram is starting to get a little confusing!
Like in the previous diagram, you should see the red numbers as being written on the outside of the sphere, and the green numbers as written on the inside. It looks like the doubling rule has turned out to be misleading — this sphere only has 14 regions, rather than the expected 16.
What happens when we keep adding circles? We could try to make another diagram, but finding all the regions might be difficult! It seems easier to let reason take over at this point, and give the pictorial part of the brain a rest.
How can we do that? One powerful fact we have is that two great circles intersect at two points. It’s not quite clear how to use this, though. Fortunately a lot of the hard thinking in this problem has already been done in the form of the Euler Characteristic.
We can define an intersection point of two great circles to be a vertex (V), and call any circular segment connecting two vertices an edge (E). Then the regions bounded by edges will be called faces (F). Euler’s polyhedron formula promises that our sphere (with any number of great circles) will always satisfy:
So far we have:
Diagram 1: V = E = 1 and F = 2
Diagram 2: V = 2, E=4 and F = 4
Diagram 3: V = 6, E =12 and F =8
The values of V,E and F for the 4th diagram aren’t so obvious. Let’s try to figure them out carefully, so that our eyes don’t play tricks on us.
Pick one circle to focus on. This intersects each of the other three circles in two places to generate 3×2=6 vertices. Now, ignoring this circle and picking another circle, that circle intersects each of the remaining 2 circles in 2×2 = 4 new vertices. Now throwing that circle out as well, there are two circles left, contributing a final 2 new vertices, for a total of 6+4+2 = 12 vertices.
We can count edges too. Fix your attention on just one circle. Notice that it should contain 6 vertices, two for each of the other three circles (because it intersects each of these twice.) A circle with 6 points on it is divided into 6 pieces. Therefore each circle contributes 6 edges, for a total of 4×6 = 24 edges.
I don’t know a simple way to reason out the number of faces, so let’s just say that by inspection we found that there were 14.
Notice that for each of the four diagrams, the Euler Characteristic formula for the sphere (vertices – edges+ faces = 2)
applies:
Though counting faces seems to be hard, we can count edges and vertices for any number of circles fairly easily. This means that we don’t need to count faces, because the Euler equation easily gives . All we need to know is the formula for the number of edges
and the formula for the number of vertices
.
Following the reasoning we used for the 4th diagram, if there are great circles, then the number of vertices will be
Similarly, there will be
edges. We can now find the number of faces by using the Euler Characteristic:
or
This tells us that the number of regions into which great circles divide the sphere grows roughly as the square of the number of circles. We can also compute particular values. Though no one would probably ever want to count to check, with
great circles, there are 9902 regions.
This completely solves the problem of region counting with great circles on a sphere. What’s next?
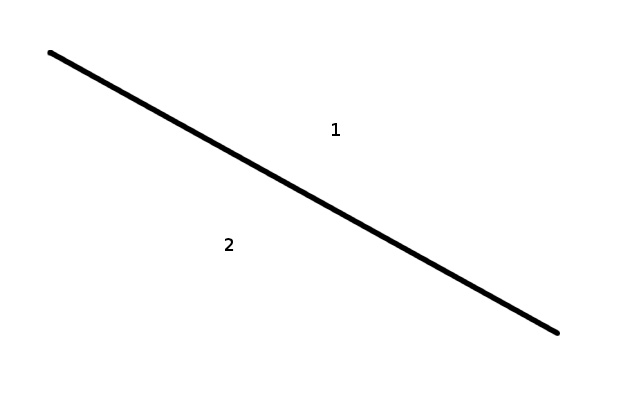
We now want to move away from the sphere for a moment and ask a seemingly unrelated question about arrangements of lines in the plane.
Just like we only used great circles in the sphere, we only want to consider “nice” arrangements of lines. We don’t want any of our lines to be parallel, or any three of them to intersect at the same point. Our line configurations are supposed to be “generic”– what you would get by picking a bunch of lines randomly.
Now, let’s try to play the region counting game with the plane. Here are some pictures to get us started.
It’s clear that the plane is giving us values that are different from the sphere. The numbers 1 (for no lines), 2, 4, 7, and 11 may at first seem to be random, but there is a subtle pattern. These numbers can be seen as coming from Pascal’s triangle:
In Pascal’s triangle, the entry in row and column
comes from summing the entries directly above and to the left of it. For example, 35 = 15+20, and 10 = 6+4.
We are looking for a way to connect the entries in the number sequence 1,2,4,7,11 to the entries in Pascal’s triangle. We can do this as shown here:
If you sum the elements in the first three columns in each row of Pascal’s triangle, it produces the number sequence 1,2,4,7,11,… which perfectly matches the sequence we got by making regions in the plane. If you experiment, you will see that the pattern continues to work even for . Could this pattern give the number of regions in any arrangement of lines?
Our experience with trying to guess the number sequence for the number of regions in the sphere should have made us cautious.
How can we go about finding the formula for the number of regions made by lines in the plane?
Maybe we can use the Euler characteristic again. Unfortunately it’s not clear how, because the lines in the plane are infinite, and anyway if you check you can see that the formula
no longer seems to hold. At the same time, it doesn’t seem like the plane is so different from the sphere. In fact you can connect the two using a technique called stereographic projection.
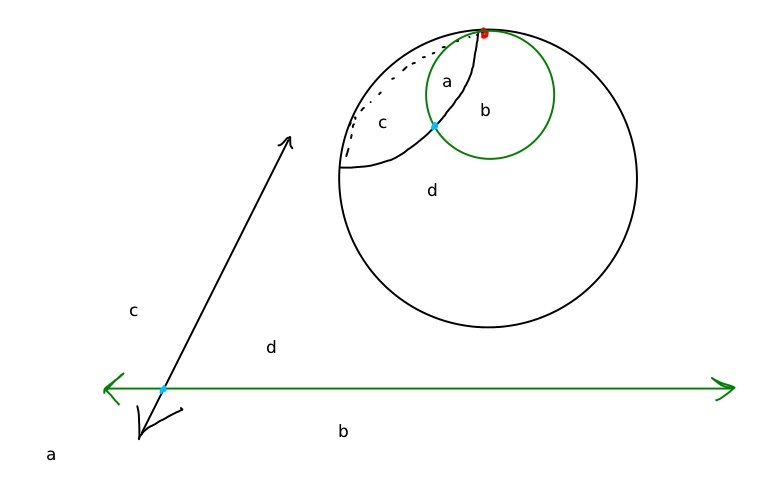
Stereographic projection gives a way to map the sphere onto the plane (which we imagine as being beneath the sphere). The idea is that there is an infinitely tiny “lighthouse” located just at the north pole of the sphere. This tiny lighthouse shines through the sphere and “projects” all of its parts onto the plane beneath. Notice that points on the sphere which are close to the north pole get sent very far away, and that the north pole itself never gets mapped to the plane.
What kinds of curves on the surface of the sphere will get mapped to lines in the plane? If you think about this for a second the answer will probably come to you: circles (not necessarily great circles) on the surface of the sphere which pass through the north pole become lines in the projection:
This is difficult to draw, so please forgive my crude figure. The diagram above shows two circles on the surface of the sphere being mapped to lines under stereographic projection. The letters indicate how regions on the surface of the sphere (resulting from the arrangement of circles) translate to regions in the plane (resulting from the corresponding arrangement of lines. )
It is fun, to explore this line making machine. How do you get parallel lines in the plane? Perpendicular lines? A moment’s thought should convince you that parallel lines in the plane “are” exactly the circles on the sphere that never intersect (except at the north pole). Since we are only working with “nice” arrangements of lines, parallel lines are not allowed–we only need to be aware of them to avoid them.
It probably will not even occur to you to worry that the number of regions you get on the sphere with circles through the north pole is different than the number of regions you get in the plane with the corresponding lines. The picture makes it pretty plain. You can shore up your doubts by reflecting on the fact that stereographic projection is continuous, and so it preserves connectedness of things like line regions.
Now, we can answer our question about line regions in the plane by using the Euler Characteristic on the sphere again! In fact, if we just remember to add one extra vertex (for the north pole) we can just count edges and vertices in the plane.
So our new planar formula is :
or in other words
Now, each line intersects each other line exactly once, and this breaks each of the lines into
pieces. Therefore
The vertices can be counted as follows. Fix one line. It intersects each of the other lines. This gives
vertices. Now discarding this line (to avoid double counting) and repeating this argument on the “next” line, we get
more vertices. Continuing in this fashion, the number of vertices must be
Putting everything together,
or
This can also seen to be equal to the first three binomial coefficients , confirming the conjecture about Pascal’s triangle.








The calculations were really complex and difficult to understand for the first time
Thank you very much sir you made a great article I agree with you and I hope you will continue to make more articles like this Thank you so much sir
Thank you very much sir you made a great article I agree with you and I hope you will continue to make more articles like this Thank you so much sir
amazing post
big hash web
nice
Hi there,
did you know this is a good and informative article, i like it. i will share this along to all my frind… you doing great job guys….
Thanks for your information & good luck to you
Resep Masakan
دانلود آهنگ وای مامان ولم کن مگه گرفتمت میمیری نگی نگفتمت چالش اینستاگرام – – متن اهنگ Vay Maman Velom Kon جوان موزیک + new music اصلی کامل مامان ولم کن مگه گرفتمت jafar-171@
ooo its cool
thanks you for article
Good luck to you anda thanks for your information
فروشگاه کاشانه
beauty fulll
Gogoherbs supplements
greatest post
آهنگ جدید گرشا رضایی مگه پاییز اومده Download New Music Garsha Rezaei – Mage Paeiz Oomade اهنگ اگه بارون بزنه با یاد تو دیوونه میشم مگه پاییز اومده jafar-167@
I’m going to ramble on a bit about some fun pictorial counting games, with no particular point in mind, except to show some pretty relations.
https://www.sourcingcompanies.com
دانلود جدید ترین قسمت سریال قبله عالم
https://pishgammovie.ir/iranian-serial-download/ghebleh-alam/
دانلود آهنگ های جدید ایرانی و خارجی شاد و ریمیکس آهنگ جدید jafar-158@ fit it now
Good Information and thank you
Nice circle to project
The circle on the sphere in the figure is a complete
دانلود آهنگ مازندرانی غمگین – اهنگ های عاشقانه غمگین مازندرانی جدید گلچین اهنگ های غمگین و شاد مازندرانی. آهنگ مازندرانی غمگین jafar-153@
دانلود آهنگ چشم نظر از مجید رضوی با گیتار ریمیکس ورژن گیتار معروف عاشقانه احساسی برای همسر آهنگ چشم نظر مجید رضوی با گیتار jafar-109@ hum. ok im redy to learn it
Loving the information on this website, you have done great job on the posts.
دانلود آهنگ جدید سعید شریعت جنون – – متن اهنگ از Saeed Shariat Jonoon تابان موزیک + new music اصلی کامل tabanmusic.com سعید شریعت جنون jafar-126@ ooh nice learn. it is neccary.
but a cant login to courses please check my payment
دانلود آهنگ ریمیکس حرف اول اسمت گردن من تا ابد حمید حسام ریمیکس حرف اول اسمت jafar-125@
Thank you very much sir you made a great article I agree with you.
Awesome article, thank you
goood luckk
thanks for sharing
greatest
goood luckk
دانلود آهنگ ساسان آران شما آهنگ شما ساسان آران jafar-90@
دانلود آهنگ مرتضی سرمدی وابسته آهنگ وابسته مرتضی سرمدی jafar-86@
دانلود آهنگ سالگرد ازدواج عاشقانه آهنگ سالگرد ازدواج jafar-51@
بهترین و بروز ترین منبع اهنگ های ایرانی و فرزاد فرزین آهنگ فرزاد فرزین jafar-93@
دانلود نوحه جدید فارسی و سوزناک جدید ماه محرم 1400 دانلود نوحه جدید jafar-18@
آهنگ شاد شمالی مازندرانی آهنگ شاد شمالی jafar-50@
آهنگ مازندرانی لاتی تک دست زندونی آهنگ مازندرانی لاتی تک دست jafar-26@
دانلود آهنگ های جدید ریمیکس ایرانی و ریمیکس خارجی باکیفیتبالا ریمیکس ماشین بیس دار آهنگ ریمیکس jafar-16@
thanks for posting great
thanks for sharing
دانلود آهنگ های تولدت مبارک دخترم و عاشقانه شاد دخترم تاج سرم آهنگ تولدت مبارک دخترم jafar-6@
Thank you for some other magnificent article. The place else may just anybody get that type of information in such a perfect means of writing? I’ve a presentation next week, and I’m on the look for such information.
Select Start > Programs or All Programs > Samsung Printers > Samsung Easy Document Creator > Samsung Easy Document Creator.
The Samsung Easy Document Creator interface is comprised of various basic sections as described in the table that follows:
Samsung Easy Printer Manager Download
thank you very useful infogood informationI will try it.
This website is designed for our students and families.
Nice article
Thank you very much sir you made a great article I agree with you and I hope you will continue to make more articles Teknoyu
enjoy
thanks for sharing
Great post thanks for sharing this information with up!
Thankyou for your information gaes.. next again
thanks u for article
Infonya sangat menginspirasi
nbice and hard work thanks for help
jafar-63@
math very inportant on any science , but need more inteligence
دانلود آهنگ شهرت ممدوف اوپوم نفسیندن آهنگ اوپوم نفسیندن jafar-27@
Thank you, I like this information.
thnaks
دانلود آهنگ سلمان خان هندی جدید شاد رقص سلمان خان فیلم های هندی جدید 2020 شاد خفن تخیلی خواننده زن و رقص سلمان خان دانلود آهنگ سلمان خان e825130
thanks artikel
thanks for you sharing sir
Thank you sir.
this is very helpful.
thanks again sir
thanks boss.
i like this post
thanks a lot sir
Thank you great artikel
I have an math table for child. Thansk for sharing.
Infonya sangat bermanfaat dan mengedukasi
thanks u for article
helpfully blog for everyone…
Pembelajaran yang sangat bermanfaat
never read like this..nice article
nice..i love to read it
Thank you very much sir you made a great article I agree with you and I hope you will continue to make more articles like this Thank you so much sir
Rerciver Option!
دانشمندان معتقدند گوش دادن موسیقی مناسب به افزایش تمرکز کمک میکند
اما اینکه به چه مدل موسیقی گوش دهیم جای تفکر و بحث دارد.
آهنگ کردی که از آهنگ های اصیل ایرانی است طرفدار بسیار دارد. با گوش دادن به موسیقی های اصیل ذهن خود را به کلمات اصیل و ناب بسپاریم .
Amazing one
Good one
Nice one
nice artikel good posting i read full of detail your grammar very perfect
hai..its great to read
thank you very much. this article is very helpful.
آهنگ شاد کرمانجی عروسی دانلود جدیدترین آهنگ های کرمانجی دانلود آهنگ جدید و قدیمی کرمانجی دانلود اهنگ رقص و عروسی محلی کرمانجی جدیدترین آهنگهای کرمانجی آهنگ شاد کرمانجی عروسی 8f1de2c
آهنگ جدید شاد با صدای خوانندگان برتر و پرطرفدار ایرانی به همراه ریمیکس شاد و بیس دار با بالاترین کیفیت ممکن # دانلود آهنگ شاد 9a3ae97
آهنگ جدید شاد با صدای خوانندگان برتر و پرطرفدار ایرانی به همراه ریمیکس شاد و بیس دار با بالاترین کیفیت ممکن # آهنگ جدید شاد f93b683
thanks for good article
thanks u for article
thanks u for article
This website is designed for our students and families. It will provide information on what your child is learning in math, activities you can do at home to reinforce. Thanks
Regards,
Bunga Papan
Thanks for your information & good luck to you
I love this material :* thanks for share it Berita Teknologi
I have matematik materi there Dompet Kulit
greet artikel, I must studying it :v
Pingback: The Won’t Stop Round Up : Footenotes