The feelings that I associate with Quaternions (which I will persist in capitalizing, as an homage to their 19^th century origins) are not really professional. I see them as a Victorian curiosity; the kind of thing that might be referenced in an Alan Moore comic, or kept under a bell jar in some museum with lots of wainscoting.

For the non-mathematical reader, the Quaternions are something like the complex numbers, except that they have three imaginary elements instead of just the usual . For me this gives them a kind of Spinal-Tap like property of super-abundance – this number system goes up to three.

Whereas in the complex numbers we have to be satisfied with only one weird relation, namely , in the Quaternions we get three times the mystery. In addition to , there are two new letters and with the property that

.

William Rowan Hamilton

The inventor of Quaternions, William Rowan Hamilton, carved this relation into Brougham (Broom) Bridge in Dublin, where he happened to be when he had his revelation.

A person who hasn’t had a year of Abstract Algebra may be puzzled as to why Hamilton’s relation is better than any other relation you might make up with some letters from the middle of the alphabet.

Why not achieve mathematical immortality by advancing the more awesome looking relation

?

The miracle that occurs in Hamilton’s relation is that the product (and quotient) of two Quaternions is another Quaternion.

For instance if you multiply out and , using the normal rules for multiplying multinomials, you get

Using Hamilton’s relation, this simplifies to

or in other words the Quaternion

Something similar happens when two Quaternions are divided.

Who cares? One reason to care is that providence didn’t equip the universe with too many systems like the Quaternions. They are one of a small beastiary of magical structures. If you’re looking for something that you might naturally call a “number system” (with finitely many dimensions) that contains the real numbers, your options are four (Hurwitz’s theorem):

Here is the real numbers, is the complex numbers, is the Quaternions (after Hamilton), and are the octonions. Each of these contains all the previous systems as a subsystem, so that the most universal is , and the smallest is . They also get progressively more strange, and their multiplication becomes harder to recognize as “multiplication.” For instance in you lose the property that and in you lose even the property that . In other words in you can’t talk about the product of three “numbers” unless you say exactly in which order you want to multiply them. In the multiplication we’re used to, “the product of 8, 6 and 4” is completely unambiguous. It is 192. But in other number systems, yelling mathematical phrases across the room would require a lot more caution and precision. You might say, “Take 4, multiply it on its right by 6, and then multiply that result on the left by 8.” And this would be necessary for the answer to be unique.

You can argue for the importance of the Quaternions on the grounds that they are “God given,” appealing to the special nature of , and the above fact about “normed division algebras” extending the real numbers. A mathematician can show that is special, provided you accept that the counting numbers are special.

It seems plausible to say that any alien race that “counts” in the same way we do would eventually have their own Hamiltonian epiphany on Brougham Bridge, despite the fact that that bridge might be made of singing crystal and arch over a body of sentient lava, etc.

But maybe this kind of “center of the universe” argument isn’t to your taste. Ironically the arrival of the Quaternions on the intellectual scene was quite disturbing. It was part of a wave of new systems (new geometries and algebraic systems) that made mathematicians question the value of traditional mathematics, and its role as the ultimate in apodicticity. Kline compares this to the way in which a person might reevaluate his cultural mores (and their claims to being absolute) after a trip abroad. In fact Kline posits that Non-Euclidean Geometry and the Quaternions were the two bullets that destroyed humanity’s optimism for finding truth in any field. (Because if there is no truth in math, then where might it be?)

But there are other reasons the Quaternions are cool.

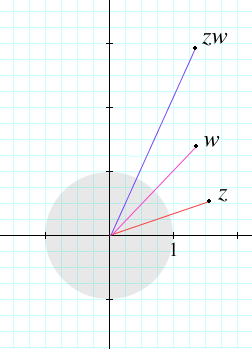
You may know that multiplication of complex numbers has a geometric meaning. If I take two complex numbers and , I can think of them as points in the complex plane. The “number” is the location and the “number “ is the location . When I multiply the two of them I get a new number/location by

Is there a simple geometric relationship between what I got and what I started with? Yes. The number/location is the point that you get by adding the angles that and make with the real axis, and multiplying their magnitudes (distance from the origin).

Complex multiplication

In fact it’s fun to play this game: Take a complex number, like, say, , and repeatedly raise it to higher and higher powers. If you plot the corresponding points, you will see them “spiral away” from the origin in a satisfying fashion.

From this discussion you can see that the complex numbers have a geometry that’s closely tied to their properties as a number system. Multiplication is the same as spiraling. Adding has a pretty geometric meaning as well. The system is inherently two dimensional.

The inherent dimension of the Quaternions is 4. This makes it harder to visualize what happens geometrically when Quaternions are multiplied. Okay, it makes it impossible to visualize what happens when Quaternions are multiplied. But they can be used to describe rotations in 3 dimensional space. The easiest way to understand how this works may be to read this very good summary (and beware the less than lucid Wikipedia)

What Hamilton was trying to do actually, that day on Brougham Bridge, was come up with a 3 (not 4) dimensional analog of the complex numbers. This was a 19^th century preoccupation, and so it is a testament to Hamilton’s ability that he is the one who finally broke through (evidently Gauss did something similar, but never published his thoughts.) It’s true that Hamilton missed the mark by a dimension, but by Hurwitz’s theorem he had no choice. An excellent explanation of why a 3 dimensional solution is impossible is given here.

The Quaternions had a vogue in which they were studied intensively in mathematical circles that lasted approximately fifty years. Many eminent physicists, including Maxwell, used them in their work. Intuitions developed from the Quaternions served as a basis for the theory of vectors, which eventually supplanted them. There was even a Quaternion Society, at the beginning of the 20^th century. As everyone knows who has been to math graduate school, Quaternions eventually decreased in relevance. Other methods, less specifically attached to 4 dimensions, were developed and took over the role of Quaternions in applications, notably the vector methods developed by Grassmann at approximately the same time. It would be easily possible to get a degree in mathematics today and never encounter the Quaternions, or else visit them only as a relic, the way a student in biology might get to palm a bezoar, or a student in engineering might tweak a Stirling engine.

But with the advent of 3 dimensional computer graphics, Quaternions as a scientific tool came back to life. They provide advantages over other methods for computing rotations in 3-space, notably numerical stability and the avoidance of gimbal lock. You can easily find down to earth explanations of how to use them in practice, such as this one.

A survey of the organizations hosting information on the subject can be found here.

Hamilton devoted much of the rest of his life to Quaternions.