1. Mixed numbers, the spittle on the front steps of our oh-so-coherent-and-sensible mathematical edifice
I learned to loathe mixed numbers, such as  , after dealing amicably with them for thirty years or so. It was on the Appalachian Trail, I was a new-ish grad student and adjunct at CUNY, and I was hiking and talking about teaching math with friend and mentor Roman Kossak. Perhaps you have some inkling why I feel this way — maybe you’ve suffered the same realization — but if not, beware: the following thoughts, once thought, cannot be un-thought. In our discussion, Roman indicated his dislike of mixed numbers and I expressed my surprise, so he asked the following question:
, after dealing amicably with them for thirty years or so. It was on the Appalachian Trail, I was a new-ish grad student and adjunct at CUNY, and I was hiking and talking about teaching math with friend and mentor Roman Kossak. Perhaps you have some inkling why I feel this way — maybe you’ve suffered the same realization — but if not, beware: the following thoughts, once thought, cannot be un-thought. In our discussion, Roman indicated his dislike of mixed numbers and I expressed my surprise, so he asked the following question:
In the number  , how are the quantities
, how are the quantities 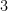 and
and 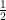 connected?
connected?
In particular, what operation sits between them? From early in our mathematical lives we are drilled on the following convention: when two quantities (terms, expressions, etc.) are written next to each other, with no operation in between, then they are connected by multiplication. But this is clearly not the case with mixed numbers — if we multiply 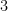 and
and 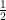 , we obtain
, we obtain 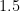 , but
, but  is equal to
is equal to  . They are connected by addition. What? What the what? I’ve hated mixed numbers ever since (not the numbers themselves, which are fine and even useful — splitting up the whole number part and fractional part of a number can be quite handy! — but the abomination that is our current notation).
. They are connected by addition. What? What the what? I’ve hated mixed numbers ever since (not the numbers themselves, which are fine and even useful — splitting up the whole number part and fractional part of a number can be quite handy! — but the abomination that is our current notation).
2. PEMDAS and dividing rational functions
I could go on an on about the order of operations and the accompanying mnemonic PEMDAS (in reality, something like PE(MD)(AS)), but for now I want to focus on the MD. The rule here indicates that Multiplication and Division have the same precedence, and when a number of multiplications and divisions occur in a row they are to be evaluated from left to right. This means that when confronted with the expression:
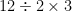
we should first divide 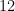 by
by 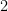 , and then multiply the result by
, and then multiply the result by 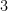 , yielding and answer of
, yielding and answer of 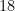 . This is tricky enough for someone wrestling with these ideas, since the “general notion” is that we carry out the operations according to the order they appear in PEMDAS, which would seem to indicate that we do the Multiplication first. However, this kind of discrepancy can be singled out and emphasized to students when they first encounter it, without (too much) harm. My problem comes a little later in the curriculum, when we confront division of rational functions — and, in particular, when the second function consists simply of a term. An example of such a problem might appear like this:
. This is tricky enough for someone wrestling with these ideas, since the “general notion” is that we carry out the operations according to the order they appear in PEMDAS, which would seem to indicate that we do the Multiplication first. However, this kind of discrepancy can be singled out and emphasized to students when they first encounter it, without (too much) harm. My problem comes a little later in the curriculum, when we confront division of rational functions — and, in particular, when the second function consists simply of a term. An example of such a problem might appear like this:

How are we to interpret it? The intended meaning, and the way the problem is inevitably presented, is that the first fraction is divided by the second expression, like so:
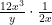
This interpretation is quite pervasive — an informal poll of colleagues and graduate students shows just-about-universal agreement. But following PEMDAS and taking the previous example as a guide, the correct simplification is:
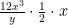
Once again, WHAT?
Many thanks to my colleague and friend Thomas Johnstone for pointing this out and discussing it with me ad nauseum.
3. More order of operations nonsense
Consider at the following two examples:


Most mathematicians would agree that, in the first expression, we are meant to first multiply  , and then evaluate
, and then evaluate 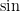 of the result. In the second expression, we first evaluate
of the result. In the second expression, we first evaluate 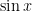 and
and  , and then multiply the results. Onscreen, the typsetting power of LaTeX gives us a visual clue, by grouping the
, and then multiply the results. Onscreen, the typsetting power of LaTeX gives us a visual clue, by grouping the  in the first example but separating the two trig functions with a bit of space in the second — but this is subtle, and disappears entirely on the chalkboard. What kind of rule regarding order of operations can apply here? Do we evaluate first, or multiply first? Either way we have it, one of them is plain wrong.
in the first example but separating the two trig functions with a bit of space in the second — but this is subtle, and disappears entirely on the chalkboard. What kind of rule regarding order of operations can apply here? Do we evaluate first, or multiply first? Either way we have it, one of them is plain wrong.
Rant follows
TL;DR: This situation is crazy!
We teach the general rules, and we give examples of how they work in practice. We hope the rules make an impression on malleable brain matter, but the examples are the heart of how our students learn (perhaps this changes as they move into the upper reaches of our mathematics curriculum, but perhaps not). Enough examples, and they start to internalize them and extract some version of the general rule of their own accord. If the examples are good enough, varied enough, and consistent enough then hopefully “their version” of the rule will more-or-less agree with “the rule.” If the examples don’t follow the rules, what the heck are our students supposed to do, anyway?
Surprisingly, the discrepancies between these examples and the rules they purport to follow never bothered me before someone pointed them out — I would solve these problems according to the examples I had been given, without questioning the discrepancies between the examples and the rules. Some of these examples are completely inculturated, and have been integrated into our mathematical canon (mixed numbers, for example). Some exist more-or-less in “blackboard world,” a special realm in which the typesetting conventions of textbooks don’t always apply. Some are simply accepted without a thought. In some cases, there is disagreement (even among major software implementations of mathematics, such as Excel vs. Mathematica). Despite the common argument that mathematics is a language, perhaps the one pure language — rational, rule-based and unambiguous above all — it seems it seems it is infected with the same kinds of exceptions, special cases, and nonstandard usages that plague our students in their English classes. What’s to be done? And more to the point, what are our students meant to do with this (aside from carrying on, in much the same way as always)? Your suggestions are most welcome…






