The urgent need to rethink the meaning of “understanding” in general, and in particular of “understanding in mathematics” has arisen in the context of specifying the Student Learning Outcomes in remedial and entry college level courses of mathematics. The template of SLO assessment sent out to Mathematics Departments of Community Colleges at CUNY has explicitly removed the phrase “understanding” from SLO’s under a misguided, if not outright incorrect assumption that it can’t be measured, as the grapevine coming to the departments informs. Jon Star of Harvard’s GSE proposes assessment of understanding based on critical thinking and reasoning @http://gseacademic.harvard.edu/~starjo, even in the multiple choice format. But that’s Harvard U, which together with Caltech, MIT and other institutions of similar type are excused from asking for “understanding”. Not CUNY. The time when CUNY was known as the Harvard for the poor seems to be irretrievably lost in the past. That tendency is not, of course limited to our university. A recent conference of all six community colleges of the Hawaii University held in Honolulu last spring had revealed exactly the same top down command of excluding “understanding” from their assessment procedures.

So what is “understanding”?  All of us know it. Any “Aha” moment is the moment of understanding. Since all of us know it, we are to large degree aware that it is a moment when suddenly things start making sense and that means that their relations with each other are very clear.

Wikipedia suggest the following sentence as the “other” meaning  of “understanding”: Understanding is the awareness of connections between individual pieces of information. Cognitive psychology, and in particular developmental cognitive psychology defines understanding of a concept as thinking focused on investigating and utilization of connections between different particular manifestations of the concept in question, that is its schema, the network of relationships.

What kind of thinking is it?

It’s worthwhile to listen to the professional of thinking, A. Einsten, who on the p.7 of his Autobiographical Notes asks a similar question. “What exactly is thinking? When at the reception of sense impressions, a memory picture emerges, this is not yet thinking, and when such pictures form series, each member of which calls for another, this too is not yet thinking. When however, a certain picture turns up in many of such series then – precisely through such a return – it becomes an ordering element for such series, in that it connects series, which in themselves are unconnected, such an element becomes an instrument, a concept.”

Piaget, who together with the physicist Garcia of Mexico, investigated the development of  conceptual schema in mathematics and sciences (Piaget and Garcia, 1989) agrees in general outlines with Einstein’s description. The authors point to the fact that essentially there are three levels of schema formation, that is of the process of understanding, the first one is the familiarity with the individual pieces, those “memory pictures” –  the- intra process. The second stage is the reflection and investigation of relationships between the different pieces – the inter level, or that moment in Einstein’s description when “such pictures form series, each member of which calls forth another” indicating that some relationship between individual pieces of information has been established. And finally when the reflection upon the discovered relations blossoms into the grasp of the underlying structure of the developing concept, when “ a certain picture turns up in many of such series then – precisely through such a return – it becomes an ordering element for such series, in that it connects series, which in themselves are unconnected…”, we have              the trans stage of understanding the concept, which transcends the boundaries imposed by its particular manifestations.

All of this is simpler than it sounds. Starting in the early childhood, when the formation of earliest concepts such as a table, a chair, water takes place, exactly the same process of their development as described by Einstein takes place in every child (Skemp, 1977, Vygotsky 1986). First are isolated impressions of different fragments of the chair, then its mutual usefulness and roles, and finally, the chair is grasped as a full, operational concept.

Can this process be measured? Can one ascertain the degree of understanding of a particular concept? Can one measure understanding?

Nothing simpler than that, if one knows what she or he wants to measure, as the performance task preparing DOE/NYC teachers for the introduction of Common Core standards in mathematics shows us:

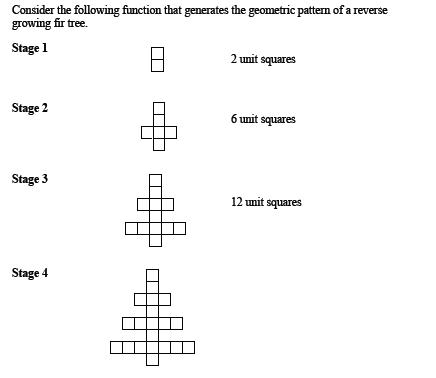
The  given figures provide first sense impressions and memory pictures as the intra-operational components mentioned by Einstein. Questions 1-3 facilitate the discovery of inter-operational relationships between the memory pictures, so that one picture brings forth another. Question 4 offers the possibility of formulating the concept of the variable which “connects the series which by themselves are unconnected”.  Question 5 can be answered either after successfully constructing the variable general term in question 4, or independently of it through extending understanding of the series, “one member of which calling forth another” for high numbered stages.  Students’ work on the problem and the degree of their success gives precise information as to the degree of understanding the concept of the variable in the context of generalization. The problem was given as an assignment for students in the Math for liberal arts course at Hostos CC. Good 20% of students reached the trans stage of formulating the general term for the series what indicates full understanding of the concept. Around 40% of students reached the inter-operational stage of recognizing the relationship between the series, some reaching mastery of that stage demonstrated by the correct answer to question 5 without using the pathway leading through the general term.

Then what is the problem? Why is really “understanding” in mathematics conspicuously absent from the SLO’s at CUNY’s community colleges and at community colleges around the country by the top down decisions, especially in the light of nation-wide failure in learning algebra as the recent NYTimes article Is Algebra Necessary?  informs? Is it an effect of the “vicious circle” described in the earlier post at https://cunymathblog.commons.gc.cuny.edu/2012/09/09/is-algebra-necessary/, is it an absence of familiarity with the research literature or is it an attempt to undermine the Common Core Standards in Mathematics, for which understanding  is one of the fundamental characteristics?