Audio engineers have known for a long time that music generated by computers sometimes sounds unnatural. One reason for this phenomenon is the absence of small imperfections that are part of every human activity. In a recent Physics Today article (July 2012), Holger Hennig, a postdoc at Harvard, and his collaborators described how they analyzed a professional drummer’s deviations from the metronome’s beats, and discovered correlations of the natural rhythmic imperfections. To characterize the correlations, the researchers performed a power spectrum analysis. The process is analogous to analyzing radio waves in the atmosphere by setting a radio to different frequencies and listening for how much power comes out at each. The drummer’s power spectrum has the form
with
. (See Technical Note below for how
is related to the autocorrelation function.) Sound sequences defined by a power spectrum are what physicists and engineers call “noise.” (Interestingly, the composer John Cage wrote in his book Silence, “what we hear is mostly noise. When we ignore it, it disturbs us. When we listen to it, we find it fascinating.”) The character of the noise changes significantly if the exponent
is altered. When
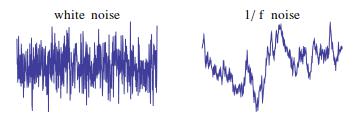
is zero, the noise, called “white noise,” is entirely random as every sound is completely independent of its predecessors. By contrast, a noise with
produces a far more correlated sequence of sounds which makes the noise rather predictable.
Hennig’s experiment and many other studies reflect the human preference for music with a balance of predictability () and surprise (
). Back in the 1970s, Richard Voss and John Clarke at Berkeley found the pitch fluctuations in Bach’s First Brandenburg Concerto to obey the
power law. This year, in a paper published in the Proceedings of the National Academy of Sciences (vol 109, pp 3716-3720), Daniel Levitin, Parag Chordia and Vinod Menon reported similar pattern for the fluctuations of written note lengths in compositions of 40 different composers. (Beethoven and Vivaldi are among the most predictable, and Mozart is among the least.)
Currently, professional audio editing software offers a humanizing feature that artificially generates rhythmic fluctuations. However, these built-in functions are essentially random number generators producing only uncorrelated white noise. The result is a rough ride: a rather bumpy, jerking rhythm. The Hennig group tried to imitate the human type of imperfection by introducing rhythmic deviations that exhibit the pattern. They prepared audio examples of a Bach’s Invention and other pieces, available at http://www.nld.ds.mpg.de/~holgerh/gallery, and found that more respondents preferred the
version to its white-noise counterpart. You can listen to these samples and make a judgment yourself. Please share your thoughts by posting a comment.
Technical Note: For a time-fluctuating physical variable such as the drummer’s deviations from the metronome’s beats or Brandenburg Concerto’s output voltage, we can represent it as a Fourier integral
where the Fourier coefficient is
. (The limits of all integrations in this note are
, which we omit writing.) The autocorrelation function
is a measure of how the fluctuating quantities at times
and
are related. It can, like any other function of time, also be expressed as a Fourier integral:
, where
is the spectral density of
. This known as the Wiener-Khintchine relations. The spectral density is proportional to the square of the Fourier coefficient:
(recall Parseval’s Theorem). Nowadays it is convenient to use Maple, Mathematica, Matlab, even Excel to perform a fast Fourier transform. The above simulation of noise was produced by (inverse)-Fourier transforming the product of the power-law spectra and random numbers generated by Mathematica. It should be quite feasible to ask students to analyze actual musical performances. I personally am curious about the rhythmic pattern in Glenn Gould’s Bach.



Awesome post, informative. Also visit me at: https://luxurysupercarsdubai.com/
Hello! Any of the links on this post will take you directly to where you can purchase this product, but here is the direct link to my Multiplication 2nd Grade Mathbook! Hope that help thanks
Quality articles or reviews is the main to attract the users to pay a visit the web site, that’s what this website is providing.
https://safetottosite.jouwweb.nl/
Hi
Dignity College of Healthcare online surgical technician training is far superior to other online surgical Technician programs because it includes the training and exam review for the EKG technician (optional) and a comprehensive, but simple tailored program for the Surgical Technician. So a completion of our course enables the graduate to practice as an EKG Technician in any State of the United States, as well as practice as a Surgical Tech in any state.Surgical technician certification online
Hello,
Dignity College of Healthcare offers Surgical Technician Program Online. Register with Confidence and attend a nationally accredited, but affordable certification course. In just 4 months, you can finish with two certifications (An Electrocardiogram Technician and a Surgical technician from the school) without a loan on your neck!Online surgical tech courses
So now, you can check the catalogue for the stack number of the CD or DVD that you are interested in, pick up the jewel case from the shelf and pass it to the Loans Desk staff for the disc. Or you can skip the first step and browse the shelves for musical works that you fancy. Who knows? Serendipity may lead you to other works that are new to you!
thanks alot,
we use your fantastic information to do a similar project in matlab
Best Music Site Ever
The subsequent time I learn a weblog, I hope that it doesnt disappoint me as much as this one. I imply, I do know it was my option to learn, but I actually thought youd have one thing interesting to say. All I hear is a bunch of whining about something that you may fix in the event you werent too busy looking for attention.Visit Cape Verde
Great, great to read this article!
Thanks for sharing superb informations. Your web site is very cool. I’m impressed by the details that you have on this web site. It reveals how nicely you understand this subject. Bookmarked this web page, will come back for extra articles. You, my friend, ROCK! I found just the information I already searched all over the place and simply couldn’t come across. What an ideal website. Tool Boxes
Thank you for fantastic information I was looking for this info for my mission. I’m not certain the place you are getting your info, however good topic. I must spend some time studying much more or working out more.spotify beats
Hi,
Against Deception does up beat good fast EDM Worship Music electronic christian music Christian Trance music listen now on Pandora radio.fast beat worship songs
Against Deception does up beat good fast EDM Worship Music electronic christian music Christian Trance music listen now on Pandora radio.Christian Music songs
Always go for a mini metal lathe that will best suit your need. As we come to a conclusion, you should keep in mind that quality is often the critical aspect you should assess when choosing a product, and mini metal lathe is not any different.good fast worship songs
I love receiving gift cards, especially Sephora ones! Although I have some friends who don’t like to give gift cards because it’s so impersonal. I like gift cards because I like to choose myself what I would like instead of giving a list.Easy English
Hello! Any of the links on this post will take you directly to where you can purchase this product, but here is the direct link to my Multiplication 2nd Grade Mathbook! Hope that helps!lindie rock type beat
The great music, wonderful food, fabulous drinks, and all in a warm-hearted Americana loveliness. I can’t wait to see it for myself one day. I’ve never been to this part of the US but if this is how you party. I’m in!Ska band
First of all, pass that avocado because they’re my favorite and it looks absolutely delicious. Those microhouses look amazing – what a great concept for those whom are homeless! Great links Cassie, especially that Jurassic Park computer system hahaha taking it back! Have a great one -Iva.little desktop pets
I really appreciate your amazing blog! This is a maximum options provider to all the users and in a single place, you can look most of the techniques for how it will be used in your mobile.for blog
Hi, Thanks for sharing your informative article. I recommend my students to follow your blog posts as they give very good insights. I teach digital marketing and expect my students to read the blog posts.the iconic coupon
I find almost any music at all, even quiet music with some sort of melody to it — Clair de Lune for example — will distract me while I’m writing or grading. Ambient music is perfect, assuming you prefer it to silence, which I generally do. Pandora’s ambient channel is pretty good.unified roots nottingham
I find almost any music at all, even quiet music with some sort of melody to it — Clair de Lune for example — will distract me while I’m writing or grading. Ambient music is perfect, assuming you prefer it to silence, which I generally do. Pandora’s ambient channel is pretty good.Gem Music Producer DJ
many thanks a good deal this amazing site can be conventional in addition to relaxed.
https://musicdel.ir/single-tracks/
Hey, great job with the company, Tushei. Good Luck. The music was on point too, look forward to seeing the future videos. If you need any help with cinematography, you know who to call! Pedal Harp
This is total crap, I was brought up in the project in marble hill as well as 4 blocks away from the Apollo theatre and attended Harriet Tubman elementary school. I was one of 8 Puerto Rican families in the entire neighborhood. I saw and lived things that were horrible and that no child should ever have to be subjected to. I tell my story and have actually did some Rapping myself but profanity is an option and just because others spoke like that around you or you were brought up around that type of behavior and vocabulary does not Merritt it being necessary to share your life story . You use profanity in your music because you choose to. Let’s be honest because it not necessary at all. For more information click here
Very nice Melissa Love all the things you made, how you displayed everything. Think I might have to “borrow” some of your ideas if that’s ok? For more visit gitarre lernen für anfänger.
nice blog…i’ll follow this always
ROLLAND…we i likes this brand….exclusive branded
iam always with rolland music tools….i have rolland br-8 about 10 years ago and still working until now…
Your “Statistical Pattern in Music: Predictability and Surprise” article is great and more necessary to all drummer. I have got more idea for this best article. thanks a lot for this best idea
Pingback: Round Up! : Footenotes
I’m still reading Murakami’s 1Q84, and one of the protagonists is a math instructor/novelist. There’s a part describing when he first learned a percussion instrument in high school: “He felt a natural joy in dividing time into small fragments, reassembling them, and transforming them into an effective row of tones. All of the sounds mentally appeared to him in the form of a diagram… because the score resembled numerical expression, learning how to read it was no great challenge for him.” Your post is very fascinating, Frank. I’m also personally curious about Gould’s Goldberg Variations!