There is often a feeling that anything truly new in mathematics must, of necessity, be obscure, arcane, and require several years of study to understand.  I’d like to talk about a result that was published in the most recent edition of the Notices of the American Mathematical Society, with the somewhat-scary-title “Isoperimetric Pentagonal Tilings.”   This is cool for several reasons: First, it’s accessible to anyone, really — if you’ve ever spent a few moments staring at a tiled floor, you can get the general idea (I’ll give a description below).  Second, it’s a collaboration between Professor Frank Morgan of Williams College and a group of eight undergraduate research students (Ping Ngai Chung, Miguel A. Fernandez, Yifei Li, Michael Mara, Isamar Rosa Plata, Niralee Shah, Luis Sordo Vieira, Elena Wikner).  Third, it features the Cairo tiling which appears in our header image.  Fourth, it’s brand-new — this is a mathematical question that, a year ago, was simply unanswered.  And now we know the answer.  That’s cool!

The topic of tilings have a long history, which I will not go into.  But the idea is demonstrated in every brick wall, cobblestone street, and tiled floor — we want to fit together shapes to cover a flat surface.  Great examples of square, rectangle, and hexagonal tilings appear in the street photos in Mari’s previous post on the header image.   Now, as with many mathematical problems, the particular aspect of tiling that we want to consider today is best viewed as a game.  Here’s the game:

Tile a plane with shapes so that the combined perimeters of those shapes is as small as possible.

To make this game concrete, suppose we are sketching our tiles on a playground with chalk — what shape will require the least amount of chalk, in order to cover the entire playground?  Squares, triangles, diamonds, etc?

As is often the case, once you start playing around with a game like this you realize that it makes sense to add some additional restrictions:

1. You can reduce the total perimeter by making the shapes larger — it uses less chalk to draw a single square encompassing an entire playground than it does to break the playground up into many smaller squares.  Because of this, we insist that all shapes be the same size — that is, each shape used must have equal area.  We make a typical math-y decision: since it doesn’t matter exactly what the area is, as long as all the shapes we are comparing have the same area, we decide (arbitrarily) to make all shapes have area equal to 1.
2. Are we allowed to use more than one shape?  Well, since we’re making up the rules, we can go either way on this one — and, in fact, depending on how we decide, we get two different versions of the game, the “same shape” game, or the “collection of different shapes” game.

First, let’s talk about past results:  In 2001, Thomas Hales proved the “Honeycomb Conjecture” — the least-perimeter tiling of the plane is, in fact, given by a single shape, the regular hexagon.  This tiling is popular with board-gamers, pipe-stackers, and bees:

Settlers of Catan (board game)

Pipes stacked in hexagonal pattern

Honeycomb

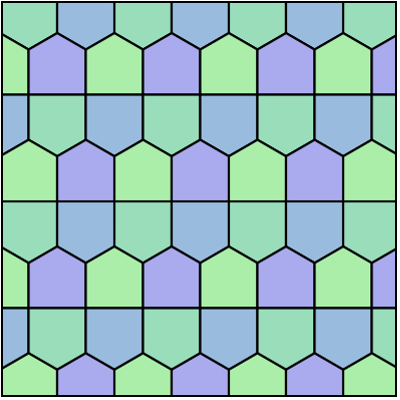
This settles the “most obvious” question, maybe, but unlocking a door is good motivation to look for another door (with a better lock)(or so goes the logic of the mathematician). Hexagons have “been done” — so what happens if restrict ourselves (obstinately) to pentagons?  Among all the different 5-sided shapes that can be used to tile the plane, which is “best” with regard to our least-perimeter game?  It turns out that here, we have a tie — the two pentagonal tilings with least-perimeter-per-unit-area are (drum roll):  The Prismatic Pentagonal Tiling, a favorite in stained-glass windows, and the Cairo Tiling, featured in our banner image above.

Prismatic Pentagonal Tiling

Cairo Tiling

Of course, any combination of these two tiles will also be “minimum perimeter” tilings — different combinations yield some great intricate examples, as discovered by Professor Morgan’s undergraduate colleagues.  Here Niralee Shah, describes their discovery of infinitely many efficient pentagonal tilings:

For more details “straight from the horse’s mouth” as it were, check out the blog post by Frank Morgan.