There are certain arguments that are beautiful and convincing but not admissible as proofs. They give the right answer, and show in an important way why something should be true, but they don’t pass muster as formal mathematics. Frequently they are shunned as “intuitive” or “heuristic” arguments that aren’t sufficiently “rigorous.” Certainly there is something about them that seems to lack deductive strength. But I am sometimes saddened by the injustice of relegating these stunning ideas to the apocrypha, especially when they served as prologue to a famous result.  It can be interesting to summon up the feeling that these arguments are “right” in a way that we perhaps do not understand.

Here I want to look at a few of these mysterious quasi proofs.

The first and probably most famous is Archimedes’ argument of the lever, which he used to find the quadrature of a parabola. Quadrature refers to the problem of finding a region bounded by straight lines which has the same area as a given curved region.  In the problem I will present, Archimedes is trying to find the quadrature of a parabolic segment. There is a very nice discussion of the problem on Wikipedia.

A picture of a parabolic segment is given here:

As Wikipedia reveals, Archimedes formally established his result using the method of exhaustion, and described his proof in a letter to Dositheus.

But in his work The Method, Archimedes establishes the result by recourse to a magical argument.

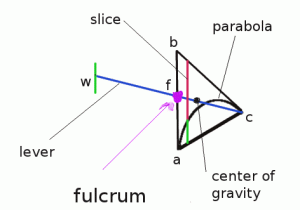
Consider the following picture.

 

We will go into the picture in detail, but the main idea is that the parabolic segment defined by the parabola and the line , when dangled from , balances the triangle which is suspended on the lever from its center of gravity.  Archimedes then concludes, from the placement of the fulcrum, that the triangle is exactly three times heavier than the parabolic segment, and therefore must have three times the area.

For those who are curious about the construction, the line containing the segment is drawn to be tangent to the parabola at .  We then draw to intersect the tangent at , with parallel to the axis of symmetry of the parabola.  This yields the triangle .

Now draw to bisect and then produce the line to so that .  Now consider an infinitely thin “slice” of which I have drawn in red and green.  Archimedes shows, using mechanical principles, that the whole slice (both red and green parts) balances at the fulcrum with just the green part suspended from .  Since this slice was arbitrarily located, the argument is completed by “summing” over all of the infinitely many slices of the triangle.

Interestingly Archimedes remarks in his argument that the slices of the triangle and the slices of the parabolic segment are equal in number. As Katz says in his book A History of Mathematics, this makes one wonder if Archimedes had some notion that there are different infinite cardinalities.

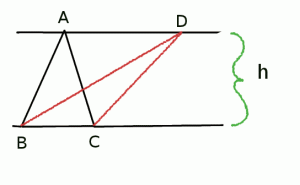
Before going on to the next magical argument, I want to remind the reader about a theorem from geometry. The idea of a “dynamic triangle” is the key ingredient in Euclid’s proof of the Pythagorean Theorem, and is given in Book I of The Elements.  Consider the following picture.

To explain the picture, suppose that a triangle is given of a certain height .  Draw a line through parallel to and on that line select a point .  Then the areas of the triangles and are the same.  It is hard not to see the triangle as a “moved” version of . This dynamic property is a powerful source of geometric intuition.

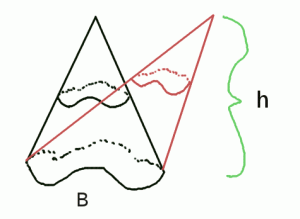
The following argument for the area of a circle was given by Kepler.

The idea is to divide the circle into infinitely many slices of pie, each one so thin that the circular segment at its base is virtually a straight line.  One then “peels” the circle as shown in the picture to form a triangle of height , where is the radius of the circle.  By the argument on dynamic triangles, each pie slice has the same area both in the circle and in the peeled version. Therefore the area of the circle and the triangle are the same.  But the triangle has height and base (because the base is the circumference).  By the familiar formula for the area of a triangle, the area of a circle must be .

Kepler’s argument naturally makes one wonder if something analogous can be done for the sphere.  Recall the following theorem on the “dynamic” properties of a cone.

Though we usually only learn the formula for the volume of a “right circular” cone, the formula is much more general.  A cone of any base and height has volume where is the area of the base.  This gives a “dynamic” picture of cone volume similar to the one for Euclid’s triangle — movements of the “tip” of the cone in the plane parallel to the plane of the base do not affect the volume.

Now (I will not attempt a graphic for this!) decompose a sphere into infinitely many cones, all meeting at the center.  To aid the imagination, suppose that the base of each cone is an infinitesimal hexagon, which is completely flat.  Now peel the sphere and lay it flat, while keeping the center unmoved.  The cones (whose volumes have been preserved) now unite to make one cumulative cone in a way similar to Kepler’s triangle.  The base of this cone will have area equal to the surface area of the sphere, and the height of the cone will be , the radius of the sphere.  This shows that the volume of a sphere should be one third its surface area times its radius, which is in fact the case, if you consider the traditional formulas:

   and  

 

Note that this uses a special property of the sphere:  all of the original cones have the same height .

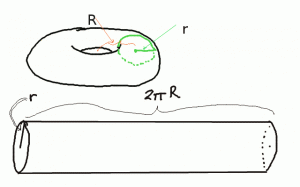
The above arguments are similar to the following magical method of finding the volume of a torus.

Finding the volume of a torus is a fairly challenging exercise for students in Calc II.  The exercise is considerably simplified if you snip the torus along the green circle and then pull it straight.  The volume of the resulting cylinder is the same as the torus. One could alternatively think of this as a “restacking” of the infinitely many discs of which the torus is composed.

 

The last example of a magical argument I borrow from Jerome Keisler‘s freely downloadable Elementary Calculus: An Infinitesimal Approach.

It is an example of something I find especially intriguing:  an infinitesimal diagram.

A version of this diagram is used in Chapter 7 to support the argument that

Here it is:

As students of calculus will know, is a small perturbation of the angle .  By the definition of radian measure (the diagram shows a unit circle) the red line in the diagram is also equal to . By imagining that is infinitely small, we can treat the red segment of the circle as if it were straight.  From basic trigonometry, it then follows that

or in other words

which is the familiar formula for the derivative of the sine function.

What do all of these arguments have in common? All of them are highly visual, and involve the infinitely small.  None of them are deductive.  There are no established axiomatic systems currently in existence that justify them.

And yet each of them is, in its own way, evidence for the truth.  From a modern viewpoint it is easy to say that these crude ideas have been replaced by the more precise idea of the limit.  But that is too dismissive of the heuristic power the arguments have to point the way towards plausible theorems.

I think something even stronger could be true, which is that the arguments are valid in the context of some logical superstructure which has not yet been discovered.  Our enormous store of mathematical knowledge has the potential to give us a kind of epistemological chauvinism.  To combat this, we should try to see ourselves as we see the mathematical figures of the past: in pursuit of something powerful, but not yet grasping its full nature.  I find it particularly humbling to consider the Egyptian and Babylonian mathematicians who could not or did not conceive of fractions with non-unit numerators, which could have greatly simplified their calculations.  There is no reason to be confident that we are not still similarly benighted.

There is a mysterious relationship between the curved and the straight, between things with magnitude and things without.  We have found deductive work-arounds for dealing with some phenomena related to these dualities, but they are still out there, and we still do not understand them.