There has been some talk in the news recently that the security provided by the RSA encryption algorithm isn’t as secure as it used to be.

RSA is an acronym standing for Rivest, Shamir, and Adleman, the individuals who designed the algorithm at MIT in 1977.

Rivest, Shamir and Adleman

An equivalent system was developed by British mathematician Clifford Cocks in 1973, though at the time he was working for a clandestine branch of the government, and his work went unattributed for many years.

Clifford Cocks

The RSA algorithm is one of the cryptographic workhorses of the internet, helping to put the “s” in “https” on the websites we use every day.  Through ingenious means, which we won’t discuss here, it is also used to produce digital signatures, which guarantee that messages originate from their specified sources.

The article linked above, concerning looming insecurities in RSA, discusses a recent talk delivered by Alex Stamos at the annual Black Hat conference in Las Vegas.  From the article it is difficult to fathom how dire the crisis might be.  It’s said that Stamos is disconcerted by recent progress made by French mathematician Antoine Joux on the discrete logarithm problem.  There is no comment from Joux, whose word I would find more definitive.  How certain can we be that the alarm isn’t an illusion?

Those things will become more clear in coming weeks no doubt.  But what is the discrete logarithm problem, and how does it relate to RSA?

We should start with a review of the ordinary logarithm function, invented by the Scottish wizard Napier in the 17th century. We then give a short description of modular arithmetic, define the discrete logarithm problem, and review RSA.  Finally, we’ll see how all these fit together, and why the ability to compute discrete logarithms quickly challenges current security protocols.

A logarithm is a function which takes two positive real numbers, a base together with an input and returns the number such that . In notation we express this by .

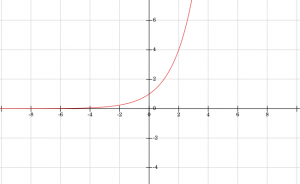
The fact that there is such a number is interesting in itself.  The existence of can quickly be confirmed by examining a graph of the exponential function.  The following figure is for , though for other values of the figure is essentially the same.  Note that for any output (on the axis) there is an input (on the axis) such that the function strikes the output with the input.  This justifies the definition of the logarithm.

The graph of the curve described by y = 2^x

To understand the discrete logarithm, it is necessary to understand the discrete context.  Here we are not concerned with real numbers, but rather with integers (whole numbers).  In fact, we are only concerned with the numbers for a fixed integer .  We can do arithmetic in this finite realm provided we are willing to “wrap around” when our sums an products go out of scope.  The exact nature of what happens is discussed in this introductory article from the Khan Academy.  If you would like something more serious, the article by Gauss himself is not difficult, and uses (in fact introduces) all the modern notation.  Amazingly I cannot find an English edition of Disquisitiones Arithmeticae online, and so I refer the reader to the excerpts found in the collection God Created the Integers.

To give a few fast examples, we write

to mean that if we were to consider stones and count them out in groups of 4, in the last pile we would have a single stone.  We call 1 the residue of 25 modulo 4. Note that if we were to take 5 stones and count them out in groups of 4, then in the last pile we would have only 1 stone.  That is, the residue of 5 mod 4 is already 1.  Note also that in this case the product of the residues is the residue of the product.  In other words, using C++ notation,

because .

In fact this is true in general, and explains many of the properties of numbers we learn in grade school.  For instance we learn that a number is divisible by 3 if and only if its digits sum to three.  I will use modular arithmetic to show why this is true for the arbitrary example of 2349. First expand using the definition of a decimal number.

Now note that and so the same is true for any power of 10.  Thus .

Now is divisible by three if and only if .  That is, it is equivalent to the condition that the sum of the digits is also 0 mod 3, or in other words that the sum of the digits is divisible by 3.  This gives something of the flavor of discrete arithmetic.

What should a logarithm be in the discrete context?  We can use the old definition, with an additional twist.  For numbers and in define the discrete logarithm (base ) of to be the number in such that .  For instance, because we know that , it follows that the discrete logarithm of 10 base 11 mod 17 is 5.

Again, we have the question of whether the logarithm is well defined.  Is it the case that for any choice of and , the integer exists such that ?  The answer is no — you should find it easy to produce a counter example.  Also, unlike the continuous cases, the discrete exponential function is not one-to-one.  This means that the uniqueness of is also an issue.

In group theoretic terms, the base now has to be a generator of the multiplicative group of integers mod in order for the definition of logarithm to make sense.  These details don’t matter for a rough discussion of discrete logs as they apply to cryptography.

Questions of efficient means of computing discrete logarithms arise in many cryptographic systems, but we will focus our attention of RSA.  At this point we need some account of what RSA is, for which I have written the this using the iPython notebook to produce an annotated example.

After following the link and diligently reading, you must now know that the crux of the RSA algorithm is the decryption step .   Can we cast this as a question about a logarithm?  Recall from the RSA example that the secret parts of the above equation are and .  The ciphertext is public knowledge, as is the modulus .  But anyone is free to encrypt a message using any public key.  This means that we can pick , and so we can know that value too.  Thus the real mystery is , the private exponent.

To find , what we need to know is:  To what power must be raised in order to be congruent to modulo ?

In other words, to crack RSA we want to know the discrete logarithm of base modulo .

For this reason, if Joux or his colleagues ever do find a fast method for computing discrete logarithms, the current implementations of many common cryptographic systems, including systems for producing digital signatures, will become obsolete.

This is not the only way to break RSA.  It seems like it should be easier in fact to crack RSA for a particular message rather than find and unravel the whole system.  To do this, imagine that the message is produced not by us but by someone communicating with the victim.  To recover we must solve for it in the equation

,

in which it is the only unknown.  This is not a logarithm problem, but is instead the problem of discrete root extraction.  In fact this problem has its own name — it is called the RSA problem.  Obviously no practical means is yet known for solving this problem either.

RSA could fall because of advances in the science of number factoring.  While this has not yet led to the gelding of RSA as far as anyone is saying, still the speed with which numbers can be factored has improved in dramatic and unexpected ways.

Shortly after RSA was announced, the popular mathematics writer Martin Gardner asked Rivest, Shamir, and Adleman for an encrypted message with which he could tease his readers.  They agreed, and produced an encoded message using a 129-digit public key.  The value of in the key was:

The prize for producing a solution was $100.  Rivest calculated, based on mathematical technology existing at the time, that factoring this number would require 40 quadrillion years.  This figure assumed a machine capable of performing 1 billion modular multiplications per second, which seems to have been achieved at the PC level only in 2009.

As this article explains, Rivest’s figures were off by many orders of magnitude, but not because he underestimated the growth in computing power.  Rather, he was overly optimistic about innovations in factoring large numbers, in particular sophisticated variants of the quadratic sieve. This article by Pomerance outlines some of the history.

For those who are curious about the solution to Gardener’s puzzle, it may interest you to know that (as a team of hackers found in 1994)

 =

The message which was encoded read: THE MAGIC WORDS ARE SQUEAMISH OSSIFRAGE

I am indebted to Julian Brown’s book The Quest for the Quantum Computer for this anecdote.  Incidentally Brown’s book is a good starting place for reading about that other perennial threat to our online security: quantum computing.