In a recent New York Times op-ed piece, Angelina Jolie revealed that she had a double mastectomy to reduce her risk of breast cancer.  She had a family history of cancer and tested positive for flaws in the BRCA 1 gene.  She wrote: “My doctors estimated that I had an 87 percent risk of breast cancer …”  Her disclosure was big news, but according to literature on judgement under uncertainty, the statistics she mentioned are likely to be misinterpreted.

While never explicitly stated, the 87 percent risk is presumably the cumulative lifetime risk.  My assumption is based on a Times article published in the following day: “Women who carry BRCA mutations have, on average, about a 65 percent risk of eventually developing breast cancer, as opposed to a risk of about 12 percent for most women…  Ms. Jolie wrote that the estimate for her was 87 percent.”

Twelve percent (for most women) is consistent with the familiar statistic that “one in nine” women would develop breast cancer.  This figure has become a mantra in the popular press and breast cancer screening programs, and has terrified many people.  (See this New York Times Magazine cover article entitled “Our Feel-Good War on Breast Cancer.”)  But what does it mean?  According to an article published in the New England Journal of Medicine, many younger women view this 12-percent statistic as a short-term probability and grossly overestimate the risk of breast cancer in a 10-year period.

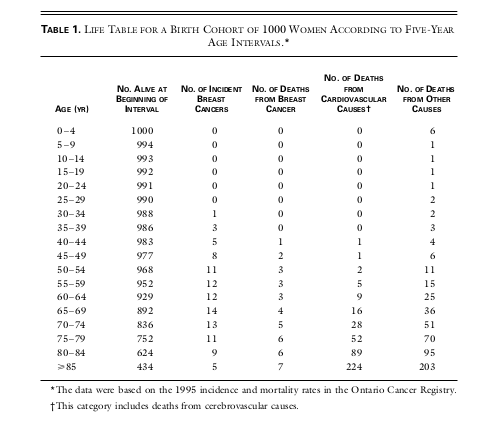
Source: K.-A. Phillips, G. Glendon, and J. A. Knight, “Putting the risk of breast cancer in perspective.” New England Journal of Medicine, 340, 141-144 (1999).

Based on the above table, we see that 1+3=4 out of 1,000 women developed breast cancer in their 30s, and 5+8=13 out of 1,000 women during their 40s.  In other words, a woman entering her 30s has a 0.4 percent chance of breast cancer in the next 10 years.  The risk of breast cancer increases with age; a woman entering her 40s has a 1.3 percent chance of the disease in the following decade.  These figures are far less than 12 percent that many people were led to believe.  Breast cancer is much more common at older ages, which makes sense.  Note that cancer incidence and cancer mortality are not the same: 1+2+3+3+3+4+5+6+6=33 out of 1,000, or 3.3 percent women will die of breast cancer by age 85.  But we also see that about six times as many women die of cardiovascular disease.  For a further discussion, Gerd Gigerenzer’s book Calculated Risks is an excellent reference.

The “one in nine” statistic is rarely explained properly, and misinterpretation fuels unnecessary levels of fear.  For this reason, the general public needs to approach Ms. Jolie’s 87 percent figure with caution.  Most importantly, her situation is not representative of what a typical 37-year-old woman would face.

Now with an understanding that 87 percent is more likely to be the cumulative lifetime risk of breast cancer for a woman (with BRCA mutations) who lives past the age of 85, the next question is what action should someone take.  There is no easy answer, as it depends on an individual’s own personal tolerance for risk, and the cost and benefit of mastectomy.  According to a study that followed up 214 women at high risk of breast cancer who had undergone mastectomy at the Mayo Clinic in Minnesota, incidence of breast cancer was reportedly to be reduced by 92 percent.  Again, we need to understand how this number was obtained.  By comparing the 214 women with their sisters who had not undergone mastectomy, about 38 were expected to develop breast cancer, but actually only 3 were actually observed.  In terms of relative risk reduction, , which is very impressive.

However, we can present the exact information in a different way.  Mastectomy prevented breast cancer incidences among 214 women, which also means that women had no benefit from mastectomy.  For some medical professionals, they prefer expressing clinical implications of the findings in terms of “number needed to treat.”  In this case, the number of patients who would need to be treated to prevent a bad outcome is then .  It has been shown that results expressed as the relative risk reduction and those expressed as the number needed to treat have different influences on decisions about treatment.

From the Book of Common Prayer, “we have left undone those things which we ought to have done, and we have done those things which we ought not to have done.”  One is frequently faced with such choices because most actions in our life do not guarantee absolute certainty.  The Mayo Clinic study demonstrates that among the high-risk group, most women (5 in 6) would not develop breast cancer even if they kept their breasts, and a few (1 in 71) would develop breast cancer even if they had their breasts removed.  For educators, I think it is important to ensure that students appreciate the meaning of probability and are able to describe risk in a variety of ways, so as they are empowered to make informed decisions by themselves.