Continuing the analysis (over-analysis perhaps) of the test, I began to wonder how students are performing on the limits portion (36 points) of the 100-point test as compared to the formula-driven derivatives portion (50 points). Certainly, the derivative is defined in terms of limits.

I have a particular fondness for limits because it is an attempt to understand infinity. I like teaching limits using an informal, visual approach at first, followed by the standard techniques for finding limits second. I end with the formal (epsilon-delta) definition and an indication of why it is needed. Teaching limits slowly and thoroughly is an opportunity to bring in some history and philosophy through, for example, Zeno’s paradoxes.

It would be good to devote a couple of classes to the epsilon-delta definition and formal proofs, but I’m not sure the broad audience in a standard calculus class is ready for it. It seems that proofs are being reduced or eliminated entirely in all the lower division math courses, but this is a topic for future post.

The overall test average was 70%.   The average of the limit portion of the test was 69%, whereas the average of the derivative portion was 76%. The students seem to be performing better on derivatives as compared to limits.  The figure below also shows this.

I like to see the histogram skewed to left. I don’t see any reason for the histogram  to have a normal distribution in a Calculus course (another post).

Now, is this a function of my tests? It is possible that I put harder limit problems than derivative problems. It would be interesting to know if other calculus instructors get similar results.

Another thing I noticed is how poorly students do on finding the derivative using the definition of the derivative. I put two such problems on the test.

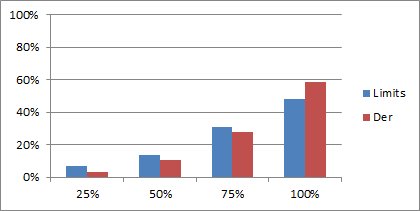
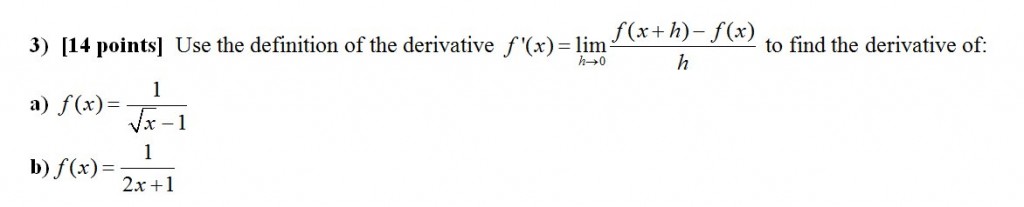The class average is only 52%, despite my best efforts at teaching this particular topic and solving more-than-usual homework problems on the board. The distribution below shows that there are a lot of students getting less than 50% on these two problems. In fact there were a few zeros.

This is not a distribution I like to see. To me it says the students aren’t learning what I would like them to learn.

However, the correlation between the limits portion of the test and the definition-of-derivatives portion is only 0.41. This low correlation says something useful. Students who don’t know how to compute the derivative using the formal definition have some confusion with the concept and notation of functions, not necessarily limits. This could be help in teaching this topic in a different manner.

I must say this is not entirely unexpected. There are a lot of things we suspect are true based on experience and folklore. It is helpful when the data confirms what we think is true, as it does in this case.