The original A Modest Proposal, written in 1729 by Jonathan Swift, was one of the most scathing and viciously ironic pieces of political satire ever (if you are unfamiliar with it, he proposes the Irish poor sell their 1-year-old children to the wealthy for consumption, thus “solving” both the food shortage and the prevalence of poverty in one dire swoop) .  So when I opened the February issue of the Notices of the American Mathematical Society and found an article with the same title, on math education reform no less, I put on my hard hat and prepared to have my ears burnt.  Here’s what I found:

First, it’s worth a read.  The author, Alan Schoenfield, professor of mathematics and education at UC Berkeley, makes an argument that is familiar but valid: that students are not being taught to solve problems but simply to carry out proscribed algorithms in a mindless fashion.  He offers some great (terrible!) illustrations of this trend, including this one (the article referenced is K. Reusser, Problem solving beyond the logic of things, Instructional Science 17 (1988), 309–338):

Reusser [2] asked ninety-seven first- and second-grade students the following question:

There are 26 sheep and 10 goats
on a ship. How old is the captain?

More than 3/4 of the students “solved” the problem,
obtaining their answers by combining the integers
26 and 10.

He gives more examples along these lines, contrasts them with some of his own more positive learning experiences, and final gets down to business:  What do we do about it?  This is the part where I retreat, turtle-like, into my protective shell and prepare for apocalypse.  Here it comes:

I truly believe that all of the mathematics in the K–16 curriculum—or at least all of the mathematics that should be in the K–16 curriculum!—can be seen as a set of sensible answers to a set of reasonable questions. My immodest proposal is that we revise the entire curriculum so that all students experience it as such, so that they come to see mathematics as a domain that not only makes sense, but as one that they can make sense of. On a more truly modest scale, I propose that we all, each time we teach, stop to think about how and why the mathematics fits together the way it does and how we can help our students to see it that way. We owe our students no less.

Does it make sense? Sure! Do I agree? You betcha!  It’s a well-reasoned, well-intentioned seed of an idea.  If this kind of revision were carried out carefully, it would do a great deal to help the abysmal situation of math education in America.  But where oh where are the dead Irish children?  Where is the shocking idea, the part that makes you snap your head and say “Wha? I can’t believe he just said that!”  The proposal is great — it’s just too modest.

My disappoint me stirred a faint memory, and (with some digging around in my files) led me to revisit this less-than-modest proposal made by Joseph Malkevitch in his 1997 article Discrete Mathematics and Public Perceptions of Mathematics.  Here goes:

Let’s get rid of Algebra.

Algebra is the mainstay of our national math education industry at the high school, and in many cases even at the college, level.   A typical student entering CityTech, where I teach, might take two full semesters of credit-bearing algebra prior to Precalculus.  Malkevitch argues that, for non-STEM majors, the emphasis on Algebra is just not worth the struggle.   If a student is going to take one college math class, let it be something relevant, something that builds problem-solving abilities and gives them the experience of wrestling with practical problems and perhaps extracting some general principles therefrom.  He makes a strong case for Discrete Mathematics as an alternative “College Math” experience, contrasting typical algebra examples, such as:

Simplify:  

With alternative questions from discrete mathematics:

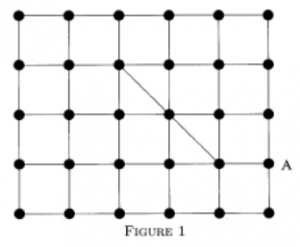
Design an efficient route for a pot-hole inspection truck, which must inspect every stretch of street in the street network in Figure 1 at least once, and which starts and ends its tour at the location marked A. (You may assume that the streets are two-way.)

He challenges the reader to consider these (and other) examples in several ways: What learning opportunities does the problem present? How accessible is it to a non-technical audience? What skills are being tested? How relevant are those skills to other areas of your life?

I highly recommend reading the first two pages of Malkevitch’s article — if they catch your attention, you’ll find the rest is worth a look as well.  I’m not ready to start crusading for Discrete Mathematics, but I’m willing to consider demoting algebra from it’s pre-eminent position.  Let’s talk about alternatives!