I gave a test a couple of weeks ago in my Calculus I class. The syllabus covered limits and derivatives. Among other problems, I always ask students to write down the derivative formulas and then give an assortment of derivative problems. Here is the relevant segment of the test:
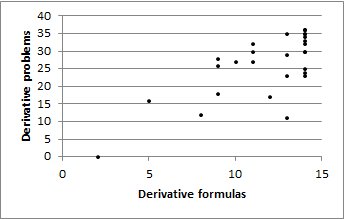
I noticed a correlation (0.72) between knowing the derivative formulas and finding the derivatives of more complicated functions correctly. Not that correlation implies causation or anything, just that there is one.
Without the outlier on the left, the correlation is 0.56, which is less, but still notable.
Would you say knowing formulas is predictive of solving derivative problems correctly on a test? Most calculus instructors would agree. It makes sense to commit to memory some of the routine formulas and rules, at least for the duration of the course, even if they are forgotten later. It becomes easier to participate in classroom discussions and speeds up doing the homework.
However, to answer the question more accurately I would have to give another class a test and allow them to have a formula sheet. Then I could compare the test scores of the two classes to see if one class did significantly better than the other. And what if one class just happens to have stronger students than the other? Then I would have to repeat the experiment several times to draw a meaningful conclusion. Still, there may be completely unexpected lurking variables.
Nonetheless, here is a correlation and scatter plot for what it is worth. I like to see that group of points on the right end of the graph. It means there are a good number of students learning what I am expecting them to learn.




maintain and strengthen our position as the world’s number one Live Casino provider as gaming markets continue to evolve globally. Our culture is rooted in our corporate values:
kingkong112233
에볼루션룰렛
Our vision is to maintain and strengthen our position as the world’s number one Live Casino provider as gaming markets continue to evolve globally. Our culture is rooted in our corporate values:
kingkong112233
에볼루션룰렛
or combination of solutions the operator chooses, the Evolution Group brand ensures the world’s best quality.
kingkong112233
에볼루션블랙잭
Whatever solution or combination of solutions the operator chooses, the Evolution Group brand ensures the world’s best quality.
kingkong112233
에볼루션블랙잭
Thanks For Sharing this useful information
전자담배 smokebomb best e-cigarette liquid site Smok25 – smoke bomb lowest price – e-cigarette – e-cigarette liquid – e-cigarette liquid site – csv e-cigarette – salt nicotine – synthetic nicotine
전자담배액상 smokebomb best e-cigarette liquid site Smok25 – smoke bomb lowest price – e-cigarette – e-cigarette liquid – e-cigarette liquid site – csv e-cigarette – salt nicotine – synthetic nicotine
I am in fact thankful to the owner of this web site who has shared this great piece of writing at here.|
바카라사이트닷컴
It touched me a lot. I would love to hear your opinion on my site. Please come to the site I run once and leave a comment. Thank you.
토토사이트
taking care to the environment is like taking care of your self too.
카지노
we are living a world where technologies are everything we can’t even go far further from it.
파워볼게임
what a nice article i found , i was looking it for a long time , i been searching it for so long now that i found out really help me.
토토사이트
Our vision is to maintain and strengthen our position as the world’s number one Live provider as gaming markets continue to evolve globally. Our culture is rooted in our corporate values:
kingkong112233
에볼루션-카지노
전자담배액상 smokebomb best e-cigarette liquid site Smok25 – smoke bomb lowest price – e-cigarette – e-cigarette liquid – e-cigarette liquid site – csv e-cigarette – salt nicotine – synthetic nicotine
Our Web Development Company in Gurgaon services will make sure the challenges you face in your business are turned into opportunities to showcase innovation.
Everyone has a natural desire to share a message with everyone, but it can be difficult to figure out how to do that.
파워볼게임
Now the easiest and traditional way of completing the home task is opening the notes in front of the eyes and answering the question given in the assignment. This is the best way of delivering the assignment on time
파워볼게임
In the prospective environment, you must do everything is about the customer engagements. Seemingly, every process and every product must implement values.
토토
Hello. impressive job. I did not anticipate this. This is a excellent story. Thanks!
파워볼
Thank for your writting. You have made it very clear that the problem is happening.
토토사이트
Everyone loves your site.. great colorations & theme. Would anyone style and design this website yourself as well as does you actually hire an attorney to make it happen for you personally? Plz reply as I!|m seeking to style my own, personal weblog and would wish to know where ough obtained that out of. many thanks
รีวิวเกม Vampire’s Charm จากค่ายเกม PG Slot ค่ายเกมที่เปิดให้บริการเกม คาสิโนออนไลน์ ที่เป็นอันดับหนึ่งของทั่วโลก โดยเกมนี้จะมีเนื้อเรื่องเกี่ยวกับ แวมไพร์ ที่มีความสวยมาก ซึ่งเกมนี้มีความน่าสนใจ และน่าดึงดูดตรงที่ ธีมของเกมสวย เมื่อคุณจะเป็นส่วนหนึ่งในการลงพนันในเกมนี้ และพร้อมที่จะรับรางวัลก้อนใหญ่จากเธอกันหรือยัง
what a nice article i found , i was looking it for a long time , i been searching it for so long now that i found out really help me.
카지노사이트
Good website! I truly love how it is easy on my eyes it is. I am wondering how I might be notified whenever a new post has been made. I have subscribed to your RSS which may do the trick? Have a great day!
바카라
전자담배액상 smoke bomb best e-cigarette liquid site Smoke Balm – smoke bomb lowest price – e-cigarette – e-cigarette liquid – e-cigarette liquid site – csv e-cigarette – salt nicotine – synthetic nicotine
I am in fact thankful to the owner of this web site who has shared this great piece of writing at here.|
토토사이트
This network is responsible for top-notch casinos like Golden Tiger Casino and Blackjack Ballroom to mention a few.
파워볼
I have read it, but the information is still less than mine, i am wanting to learn more
토토사이트
I am incapable of reading articles online very often, but I’m happy I did today. It is very well written, and your points are well-expressed. I request you warmly, please, don’t ever stop writing.
바카라사이트닷컴
Our vision is to maintain and strengthen our position as the world’s number one Live Casino provider as gaming markets continue to evolve globally. Our culture is rooted in our corporate values:
에볼루션바카라
전자담배액상 The UK Medicines Regulation Agency (MHRA) has issued drug licensing guidelines for e-cigarettes and other nicotine inhalation products that encourage and support e-cigarette liquids containing nicotine to be approved as medicines.
terima kasih telah berbagi informasi ini. semoga artikel ini dapat bermanfaat bagi pembaca selanjutnya.
전자담배 E-cigarette devices that use e-cigarette solutions are currently defined as “cigarettes that can have the same effect as smoking by inhaling solutions or tobacco solids into the body through the respiratory system using electronic devices.” Like the e-cigarette liquid, it is divided into ready-to-use and mode-to-use depending on the type of solution containing nicotine.
จีคลับ เป็นเว็บที่มีความทันสมัย ปลอดภัยสูงเข้าเล่นได้หลากหลายอุปกรณ์ทั้งคอมพิวเตอร์และมือถือผ่านทางเข้า Gclub ที่เราเตรียมไว้ จีคลับ ออนไลน์ มีเกมให้เลือกเล่นมากมาย เช่น บาคาร่า สล็อต ป๊อกเด้ง ไฮโล เสือมังกร
you have a great post and i like it.
art gallery las vegas artists
Evolution casino , the world’s No. 1 online gaming service company,
on the official website of Evolution Gaming Korea.
에볼루션카지노
Should You Tip Your 토토검증업체 메이저놀이터 메이저사이트추천 Dealer?
Thanks!
wow, its a incredible information. thanks for sharing. i think this article would be nice if you put some image to help describing the topic. Feel free to visit my website; 카지노사이트위키
앵커텍스트 키워드
I love the humor your post has offered. I enjoyed this site a lot. Keep posting article like this. It is fun. Nice photography too!
If you’re in an internet environment, you can play it anytime, anywhere.
You can always enjoy online casinos at the best timing and condition.
EVOLUTION BACCARA
thank you for your article very help me, your article highly recommended once
Renting your property can be easy with free web-based property management software which is designed to save time and money for property managers and landlords. When deciding on what platform to use, be sure to think carefully about your requirements. Spend some time researching what is available and whether or not it offers the features you need. If you find the right fit, it’ll make all the difference!it has become crucial that they deploy such a property management tool that doesn’t require too much training or technical knowledge. It should be easily deployable and bring immediate enhancement in operational efficiencies. Assess your business needs and choose the right property management software that fits well with your objectives and brings monetary advantages.
Supercross is at an all-time high in interest levels and the sport has nowhere to go but up in a time where most mainstream sports are shrinking.Feld Motor Sports has done an amazing job at making the AMA Supercross events into world-class events that are held in stadiums all over the United States.
If you’re in an internet environment, you can play it anytime, anywhere.
You can always enjoy online casinos at the best timing and condition.
에볼루션블랙잭
Evolution Casino, the world’s No. 1 online gaming service company,
on the official website of Evolution Gaming Korea.
에볼루션카지노
to boost your social media marketing we suggest you to buy instagram pva accounts
omg blog puts in a lot of effort to keep you up to date on trends from all around the world. From fashion hypes to new diet plans, exotic holiday locations or essentials for different life scenarios
It’s really great to write something like this. It’s amazing to write something that I never even thought of. 파워볼 중계 화면
to boost your social media marketing we suggest you to buy buy instagram pva accounts
Some particularly say It can for all intents and purposes be misled sometimes, but we should for the most part know that this kind of assumptions may for all intents and purposes bring out the worst of us, actually contrary to popular belief
강남가라오케.
thank you your article very help me, your article highly recommended once
Great Buy Pinterest PVA Accounts
this site is more on games enjoy clicking and have fun . 토토
This type of article that enlighted me all throughout and thanks for this.This going to be excitement and have fun to read. thank to it. check this out to for further exciting.
카지노사이트
This type of article that enlighted me all throughout and thanks for this.This going to be excitement and have fun to read. thank to it. check this out to for further exciting.
https://www.casinosite.link
That’s a great article! The neatly organized content is good to see. Can I quote a blog and write it on my blog? My blog has a variety of communities including these articles. Would you like to visit me later? keo nhacai
It’s late finding this act. At least, it’s a thing to be familiar with that there are such events exist. I agree with your Blog and I will be back to inspect it more in the future so please keep up your act 야설
Calculus is a difficult subject to learn, and I often failed exams in college.
boost your digital marketing i suggest you to buy outlook pva accounts
Backlinks are links from a page on one website to another. This is important to us and you are giving us a chance and opportunity to help each other. We are hoping to have the same goal for the future of ours. โอเล่777
ความพิเศษของเกมออนไลน์ ที่เล่นแล้วได้เงินจริง เครดิตฟรี 50 เล่นแล้วรวยทำให้คุณรวยขึ้นได้ เพียงคุณร่วมสนุกกับ สล็อต ต่าง ๆ ที่มีให้เลือกเล่นอย่างมากมาย จุใจ เล่นได้ง่าย ๆ อย่าพลาดโอกาสดี ๆ มาเล่นเกมสนุก ๆ กับเรา พีจีสล็อต และ ยังได้โอกาสลุ้นรางวัลแจ๊คพ็อตใหญ่อีกด้วยกับ เกมสล็อต พีจีสล็อต
checking through the net, Appreciation for being really thoughtful. The post contains really beneficial information. Periodico en Albacete.
to boost your social media marketing we suggest you to buy instagram pva accounts
daspdij dsovhuos
jsdj’sdd
pdsj dhovhsohv
spdojgpj jsdfpojbdx
ssjf oeuwe eofhwuo
tykytkb eyyr5rw
asdfghjkl
pwshp wswe09u
เครดิตฟรี50ไม่ต้องฝากไม่ต้องแชร์ เเค่สมัครกับทางพวกเราก็รับไปเลย เครดิตฟรี ไม่ต้องเเชร์ ทางพวกเราได้มามอบความสบายให้กับผู้เล่นที่สุด เพียงแค่สมัครกับทางพวกเรารับสิทธิพิเศษมากไม่น้อยเลยทีเดียว เเจ็คเพียงพอตคอยคุณอยู่อีกทั้ง เครดิตฟรี เล่นได้ฟรี ไม่จำกัดเวลา เล่รผ่าน โทรศัพท์เคลื่อนที่ เเละ คอมพิวเตอร์ ฝาก ถอน โอรเร็ว จ่ายตรง ให้บริการตลอด 1 วัน มั่นคง ไม่มีอันตราย ทางพวกเราจัดเต็มให้ผู้เล่นเอาใช้ผู้ใช้งานตลอด 2 ปี เล่นฟรี เครดิตฟรี 50 เพียงแค่สมัครปัจจุบัน ปริมาณ 50 บาท ด่วนก่อนที่จะหมด https://guruslot.co
Nice post. I used to be checking constantly this blog and I am impressed!
Watch Status Videos From – https://status-video.com/
I simply want to tell you that I am new to weblog and definitely liked this blog site. Very likely I’m going to bookmark your blog . You absolutely have wonderful stories. Cheers for sharing with us your blog.
This website was… how do I say it? Relevant!! Finally I have found something that helped me. Cheers!
Ücretsiz web sitesi kurma konusunda yardım arayanlara özel sıfırdan web sitesi kurulumu.
Yaş dul evlenmek isteyen bayan arkadaşlar ile üye olmadan ve ücret ödemeden tanışın.
Ümraniye içinde en uygun Ümraniye Su Tesisatçısı firması.
Çayırova ve mahallerine en yakın Çayırova Hurdacı firması.
Akardiyon makaslı çatı merdivenlerini kullanarak çatı ve teras katlarınıza güvenle çıkabilirsiniz.
Güngören bölgesinde en güvenlir, en yakın Güngöre Tesisatçı firması.
Thanks for sharing this formula
correlation is 0.56, which is less, but still notable.
Thanks for your sharing. I have more knowledge because of the posts. Your pieces of advice help me so much. They are awesome and helpful. They tell me exactly what I want to know. CBD supplements have been shown in numerous studies to alleviate chronic pain, anxiety and depression, digestive health, and more
청마담
magosucowep
tanks onturne
https://biknik.ir/tools/%d9%85%d8%a7%d9%84%d9%87-%d8%a8%d9%86%d8%a7%db%8c%db%8c/
thank you for your article very help me, thanks for sharing
An intriguing discussion may be worth comment. I’m sure you should write much more about this topic, may well be described as a taboo subject but generally folks are too little to chat on such topics. An additional. Cheers 메이저토토사이트
Email marketing is best idea to boost your marketing we sugest you to Buy old gmail accounts
Nice article and such a good information. Thanks for your excellent posting. I really enjoyed reading this blog.
Thanks for sharing the facts. You truly impressed me by this post of yours. And what exactly is additional commendable will be the authenticity in the content material.
Hi Dear, have you been certainly visiting this site daily, if that’s the case you then will certainly get good knowledge. Electrician central coast
This site is excellent and so is how the subject matter was explained. I also like some of the comments too. Looking forward to your next post. 토토커뮤니티
very interesting keep posting. 메이저토토사이트
Terima kasih, itu bacaan yang sangat keren! Custom Solutions for painting and decorating
You have done a great job on this article. It’s very readable and highly intelligent. You have even managed to make it understandable and easy to read. You have some real writing talent. Thank you. 에볼루션 카지노
You have a good point here!I totally agree with what you have said!!Thanks for sharing your views…hope more people will read this article!!! 바카라사이트
This is an interesting post that I’ll like to share with you 먹튀검증
Thank you for this information. Find latest official mobile phone prices in Bangladesh Mobile Dokan
Index Article started as a way to share what is in minds of our writers and to motivate our readers. Index article is the number one destination for Bloggers. We know our audience and what they want. You will always find honest, approachable, and relatable content here. We are open to discussion with everyone. Your point of view means a lot to us! so do visit our blogging site today.
https://www.indexarticle.com
Social media marketing is currently the most important way to express your business to your customers. Due to recent pandemic situation, the world has changed digitally, for this purpose social media accounts are really necessary. And we recommend you to buy Gmail, Instagram, Yahoo , Google Voice accounts from us at very affordable and reasonable price. Thanks! instagram pva accounts
Hello, I am one of the most impressed people in your article. 토토사이트순위 I’m very curious about how you write such a good article. Are you an expert on this subject? I think so. Thank you again for allowing me to read these posts, and have a nice day today. Thank you.
وبسایت سیگنالی تریدینگ با شرایطی ویژه سهام، فارکس، رمز ارزها یا ارزهای دیجیتال را در اختی
I have read it, but the information is still less than mine, i am wanting to learn more
카지노사이트
I simply want to tell you that I am just beginner to blogs and really enjoyed you’re web page. Very likely I’m planning to bookmark your site . You really have fantastic posts. Thank you for sharing
파워볼사이트
Thank you for sharing such a great bog it is very helpful.
토토사이트
good post
I’m so amazed together with you that will make your blog like this to be really great so we truly wanted to have a nice and interesting blogs such as this.
en iyisi
Your email address will not be published. Required fields are marked *
I like the valuable info in your articles. I’ll bookmark your blog and check again here regularly. I’ll learn plenty of new stuff right here! Best of luck for the next! Regards
The best revenge is massive success. Everyone thinks of changing the world, but no one thinks of changing himself.Don’t focus on regrets; find your inspiration in what you can do now. Live each day as if your life had just begun.
สล็อต pg 89 > เล่นคาสิโนย้งไงให้ได้เงิน วิธีที่ดีที่สุดที่นักพนันไม่ควรพลาด! รูปแบบต่างๆ ของเกมสล็อตน่าเล่น ฝาก – ถอน อัตโนมัติตลอด 24 ชั่วโมง
Every story is beautiful, but ours if my favorite
Cool you write, the information is very good and interesting, I’ll give you a link to my site. 먹튀검증
I like viewing web sites which comprehend the price of delivering the excellent useful resource free of charge. I truly adored reading your posting. Thank you! 먹튀
GG Gaming
Make Your Money More Here
Situs terbaik informasi sepakbola
Thanks for sharing this nice post.
Great post. Meanwhile, please go through Study in Italy
Thank you for sharing valuable information. Very informative article. We are share the best and real informatve about INSTAGRAM PVA ACCOUNT
proud of your efforts keep it up
amazing work thanks keep it up
Bosna hersek evlilik ve arkadaşlık sitesi ile aradığınız arkadaşı ve eşi ücretsiz aramaya başlayın.
istanbul dan kadın ve erkek arkadaş bulmak için ilanınızı oluşturun, iletişim bilginizi girin ve aramaya başlayın.
Bursa dan üyeliksiz ve ücretsiz arkadaş edinmek için arkadaşlık ilanı verin. https://bedavaarkadasliksitesi.net/bursa-bedava-arkadaslik-sitesi
Ankara Arkadaş Arama, Ankara dan bay ve bayan arkadaşlarla tanışma sitesi. İlanları incele mesajını gönder ve tanış.
Bedava evlilik ilanınızı oluşturmak için üye olmadan hemen profilinizi oluşturun ve eşinizi bulun.
H ile Meyve Sebze Bitki İsimleri, H ile başlayan bitkiler, H harfiyle başlayan meyve adları
Hint Bülbülü Ne Yer, Hint Bülbülü Ne sebze yer, Hint bülbülü ekmek yer mi, Hint Bülbülü yeşillik yer mi
We keep up with the latest techniques of building and have qualified tradesmen to ensure that your job/project is carried out safely. We also make sure that we keep to the highest standards on projects and everyone who works for us is health & safety trained.
Bihar Board 10th Model Paper 2022, BSEB Matric Question Paper 2022 Pdf Download. BSEB Board 10th Model Paper 2022 Pdf Download for Bihar Board 10th Model Question Paper 2022, Guessed Paper, Practice Paper, Mock Test Papers for Hindi and English Medium Term-1, Term-2, Term-3 and Paper-1, and Paper-2 Important Questions
Kabeh mbukak banget kanthi deskripsi tantangan sing jelas. Mesthi informatif. Situs web sampeyan migunani banget.
안전토토사이트
DMT FOR SALE exists naturally in living beings all over the world, but it has been difficult for scientists to study DMT because it does not stay in the body for long periods of time. Thanks to new advances in pharmacology, researchers are now able to inject lab rats with DMT and study its effects on their brains at will.
Medical marijuana is a hot topic these days. With the legalization of recreational cannabis in California, there’s been an increase in awareness about its medical benefits. In addition to treating chronic pain and anxiety, Buy Hemp Flower Online, medical cannabis has been shown to help with other conditions such as cancer, diabetes, Parkinson’s disease, and Crohn’s disease. If you have a qualifying condition and a healthcare provider who supports your use of cannabis-based treatments, you should be able to obtain a state-issued medical marijuana card or recommendation letter within minutes. This article will teach you everything you need to know about buying medicinal weed online in the USA.
I work to be the best at what I do and satisfy customers. You can contact me for plumbing repair.
Incoin Consultancy Services Private Limited is explicitly shaped with the end goal of Digital Signature services.
Incoin Consultancy provides digital signature certificate; Digital certificate can be introduced electronically to demonstrate one’s character, to get to data or administrations on the web, or to sign certain documents digitally. As in the current Digital world everything is going on an advanced stage. At the same time the need emerges for authentication of digital documents. Digital signatures are the answer for this. This guarantees a smooth cycle and saves the papers.
Incoin Consultancy is serving their customers with the best and exceptional service.
What I don’t understood is genuinely how you’re not, now in all actuality altogether more keenly appreciated than you might be right now. You’re so savvy. You see henceforth out and out because of this subject, made me as I might want to think imagine it from such innumerable contrasted focuses. Its like women and men are excluded until it’s something to do with Lady insane! Your own stuffs remarkable. Reliably handle it up! What’s up everybody, here every one is sharing such capacity, appropriately it’s beguiling to scrutinize this site, and I 먹튀검증
Much gratitude to you again for all the data you distribute,Good post. I was incredibly fascinated by the article, it’s exceptionally spurring I should yield. I like visiting you site since I by and large run over interesting articles like this one.Great Job, I essentially like that.Do Keep sharing! Regards . I got too much interesting stuff on your blog. I guess I am not the only one having all the enjoyment here! Keep up the good work. We are really grateful for your blog post. You will find a lot of approaches after visiting your post. I was exactly searching for. Thanks for such post and please keep it up. Great work. 먹튀검증
Amazing knowledge and I like to share this kind of information
اسکرابر
I will add a segment to my homeworks and tests to address this explicitly.
Thank you for sharing valuable information. Very informative article. We are share the best and real informatve about Signboard company in UAE
I discovered your site ideal for me. It consists of wonderful and useful posts. I’ve read many of them and also got so much from them. In my experience, you do the truly amazing.Truly i’m impressed out of this publish
Learning calculus is essential if you are a Science student. However, it is one of the tough topic to cover. There are many Android educational apps that can help to solve complex calculus math. If you want to use educational mobile apps on computer, you can check our simple guide on how to download Android apps for Windows PC.
I’ve been looking for photos and articles on this topic over the past few days due to a school assignment, keonhacai and I’m really happy to find a post with the material I was looking for! I bookmark and will come often! Thanks 😀
I simply want to tell you that I am just beginner to blogs and really enjoyed you’re web page. Very likely I’m planning to bookmark your site . You really have fantastic posts. Thank you for sharing
파워볼게임
I have been reading this blog for several months and also I am very happy to get many entries from this blog
바카라사이트
I do trust all the ideas you have offered on your post. They are very convincing and can certainly work. Nonetheless, the posts are very quick for beginners. May you please extend them a little from next time? thanks you for the post.
프로토경기결과
exceptional facts, treasured and incredible layout, as proportion suitable stuff with suitable ideas and ideas, lots of notable data and suggestion, both of which i want, thanks to offer this type of beneficial facts here. I used to be simply surfing thru the net seeking out some information and got here throughout your blog. I am impressed via the data that you have on this blog. It indicates how properly you apprehend this problem. Bookmarked this web page, will come back for greater. Really first-class and exciting submit. I used to be searching out this type of information and loved studying this one. Hold posting. Thank you for sharing. 먹튀폴리스주소
notable put up i should say and thank you for the statistics. Schooling is absolutely a sticky situation. But, is still most of the leading subjects of our time. I recognize your post and look forward to more. I just observed this weblog and feature excessive hopes for it to keep. Hold up the exquisite paintings, its tough to locate proper ones. I have added to my favorites. Thanks. Its a wonderful delight studying your publish. Its full of facts i am searching out and i love to submit a remark that “the content of your post is exquisite” notable paintings. Best publish! That is a completely best weblog that i’m able to definitively come again to more instances this year! Thank you for informative post. 먹튀검증
The article you have shared is very interesting. I am really happy that I visit your webpage, and I am agree with what you said. Please keep sharing more 에볼루션카지노
Thank you for this information. It will serve me for my exam.
Existem algumas datas de corte interessantes neste artigo, mas não sei se vejo todas elas de coração a coração. Pode haver alguma validade, no entanto, vou manter a opinião até que eu analise mais a fundo. Bom artigo, obrigado e gostaríamos de extra! Adicionado ao FeedBurner corretamente
https://www.totositehot.com
There is alot to do for digital marketing but having bulk gmail pva accounts is best because mail accounts are really the best platform to boost up your product marketing. So we suggest to buy gmail pva accounts
The newsroom’s approach to visual storytelling is not trapped inside the formats imposed upon our industry by huge platforms but stretches design boundaries and uses new technologies to tell compelling, important stories,” wrote the judges in the digital competition.
Math is always tough for me in school. Thanks for the article
Papers get to operate through Bible helpers and also plagiarism checkers to be certain that the author did not find idle at any stage in the process. Language inconsistencies won’t be a thing with your newspapers as the specialists of our school paper writing support are passionate about writing and are always excited to strike you with something fresh. By: 메이저사설놀이터
Thank you very much for the advice. Greetings.
This post is very interesting and can also be understood well. Thanks
nice share mod apk.
Metin2 Pvp Serverler
https://www.metin2pvp.gen.tr/
#metin2pvpserverler #metin2pvp #pvpserverler #metin2serverler
토토사이트
Kinda amazing and thankful finding it, so wonderful thanks to the writer .
This type of blog that’s brought big impacted to the readers, and thankful to that, click this out too.
파워볼분석
this site is more on games enjoy clicking and have fun .
카지노
¡Oye! Alguien de mi grupo de Facebook compartió este sitio con nosotros, así que vine a verlo.
Definitivamente estoy disfrutando la información. Estoy marcando y tuiteando
esto a mis seguidores! Maravilloso blog y genial
estilo y diseño.
토토사이트핫
Amazing knowledge and I like to share this kind of information with my friends and hope they like it they why I do.
Biggboss15 season is very popular Indian Tv show. The biggest salman khan television shows.Bigg Boss is back with yet another enthralling season.
bigg boss 15 mx player
I will add a segment to my homeworks and tests to address this explicitly. Bigboss 15 is very popular show in india and Pakistan,Bangladesh and all over the world.
bigg boss 15 watch online
This is an awesome show which actuallay represent the cultural behaviour of people in community.In my experience what is most critical in students being able to be successful in doing problems like those in 5.
It is hosted by popular actor suleman khan.
bigg boss 15 voot
Observe your enemies, for they first find out your faults. Bigg boss 15 is a reality tv show with highest trp in india visit here to watch it’s all episodes free.
watch bigg boss 15 online
Salman khan has announced in Bigg Boss 15 celebrities are part of this show and this show will release in september 2021.
bigg boss 15 watch online
I do appreciate that you’ve added relevant and intelligent commentary here though. Thanks! If you want to watch Bigg boss 15 visit here all hd episodes for free.
bigg boss 15 voot
Awesome keep the good work up
thank you….
thanks
very good post
It was nice to be on the website here. I will come back often in the future. Good day!강남미용실
I simply want to tell you that I am just beginner to blogs and really enjoyed you’re web page. Very likely I’m planning to bookmark your site . You really have fantastic posts. Thank you for sharing
바카라사이트
I simply want to tell you that I am just beginner to blogs and really enjoyed you’re web page. Very likely I’m planning to bookmark your site . You really have fantastic posts. Thank you for sharing
카지노사이트
kinda amazing and thankful finding it, so wonderful thanks to the writer .
토토사이트
Some truly nice stuff on this website. investigadores privados madrid
You really should experience a tournament for starters of the finest blogs online. Let me recommend this great site! Dental Office
Thankyou for this post, I am a big big fan of this web site would like to proceed updated. Dental Care
Good article! I will follow you to create useful articles like this.
Dazzling post. I Have Been examining about this issue. So a commitment of thankfulness is all together to post. Totally cool post. It ‘s incredibly exceptionally OK and Useful post.Thanks Salt Creative
รูเล็ต gclub เป็นเกมที่คาดว่าน่าจะเกิดขึ้นมาจากที่ทหารภาษากรีกโบราณนำโล่รวมถึงลูกธนูมาหมุนเพื่อเสี่ยงทาย โดยในโล่ห์จะวาดภาพต่างๆเอาไว้แล้วหลังจากนั้นก็จะหมุนโล่ห์รู้สึกว่ารูปไหนจะไปชี้ลูกไหนคนใดกันแน่ทายถูกก็ได้พนันไป วิถีทางเล่นรูเล็ตแบบย่อ คุณสามารถเลือกวางเดิมพันที่ช่องสีแดงหรือดำ หรือเลขแดงดำตามที่ใจต้องการ แล้วหลังจากนั้นวงล้อจะหมุนลูกเล็กเพื่อเสียงโชคว่าจะออกเลขไหนสีอะไร โดยแต้มพนันรางวัลที่กำลังจะได้ก็จะนานับประการในแต่ละเลข
I like viewing web sites which comprehend the price of delivering the excellent useful resource free of charge. I truly adored reading your posting. Thank you!
A human being has a natural desire to have more of a good thing than he needs. Every patient carries her or his own doctor inside. Observe your enemies, for they first find out your faults.
피망환전상
Excellent post. I was reviewing this blog continuously, and I am impressed! Extremely helpful information especially this page. Thank you and good luck. Buy acid online
Thanks for sharing this marvelous post. I m very pleased to read this article.
https://www.casinosite777.info
Hello, I am one of the most impressed people in your article. 메이저토토사이트 I’m very curious about how you write such a good article. Are you an expert on this subject? I think so. Thank you again for allowing me to read these posts, and have a nice day today. Thank you.
Diet Ron Funches Weight Loss.
Lose Belly Fat Rebel Wilson Diet.
Lose Belly Fat Beyonce Diet.
Lose Belly Fat Lose Back Fat.
Weight Loss Noom Green Foods.
Lose Weight Rebel Wilson Weight Loss 2020.
Diet Best Yogurt For Weight Loss.
Lose Weight Best Laxatives For Weight Loss.
Lose Belly Fat Ariana Grande Weight Loss.
Lose Weight Apple Cider Vinegar Gummies Weight Loss.
Lose Fat Apple Cider Vinegar For Weight Loss In 1 Week.
Weight Lose Andy Ruiz Weight Loss.
Lose Weight Amy Slaton Weight Loss.
Lose Belly Fat 50 Cent Weight Loss.
Lose Belly Fat 20 Pound Weight Loss.
Healthy Diet Weight Loss Surgery Options.
Diet Weight Loss Friendly Foods.
Weight Loss Weight Loss Breakfast Ideas.
Lose Belly Fat Weight Loss Balloon.
Weight Loss Waist Trainer For Weight Loss.
Lose Fat Victoza Weight Loss.
Diet Swimming For Weight Loss.
Lose Belly Fat Reddit Weight Loss.
Diet Rance Allen Weight Loss.
Lose Fat Quick Weight Loss Center.
Weight Loss Meghan Trainor Weight Loss.
Weight Loss Meditation For Weight Loss.
Healthy Diet Lunch For Weight Loss.
Lose Weight Low Carb Diet Weight Loss In 2 Weeks.
Lose Belly Fat Kevin Smith Weight Loss.
Weight Loss High Protein Foods List For Weight Loss.
Lose Weight Graham Elliot Weight Loss.
Healthy Diet Dr Oz Weight Loss.
Diet Detox Water For Weight Loss.
Weight Loss Collagen For Weight Loss.
Lose Fat Chelsea Houska Weight Loss.
Lose Belly Fat Bupropion Weight Loss.
Diet Best Dog Food For Weight Loss.
Lose Belly Fat Best Detox Cleanse For Weight Loss 2020.
Lose Belly Fat Best Birth Control For Weight Loss.
Diet B12 Shots For Weight Loss.
Weight Loss Antidepressants Weight Loss.
Lose Fat Achieve Medical Weight Loss.
Lose Fat Weight Loss Chart.
Lose Belly Fat Weight Loss Celebritys.
Lose Fat Tips For Weight Losser.
Diet The Free Weight Losser.
Weight Lose Weight Loss Needs.
I’ve seen articles on the same subject many times, but your writing is the simplest and clearest of them. I will refer to 메이저놀이터추천
Weight Loss Weight Loss Tips En.
Diet Rebel Wilson Weight Loss.
Diet Celine Dion Weight Loss.
Lose Weight Fast Weight Loss.
Weight Lose Before After Weight Loss.
Lose Fat Weight Loss.
Lose Weight Weight Loss Calculator.
Diet Celine Dion Weight Loss.
Weight Loss Weight Loss.
Lose Weight Adele Weight Loss.
Lose Weight Weight Loss Meal Prep.
Healthy Diet Weight Loss Motivation Quotes.
Diet Chrissymetz – Profile.
Lose Weight Tv Line Promotes Chrissy Metz Weight Loss Program – Weightlossgummies.
Diet Learn About Achieving Weight Loss With A Program Named, €Chrissy Metz†– Weightlossjourney.
Bahsegel canlı bahis sitesi
https://argus20.com
Betpas canlı bahis sitesi hizmte girdi
https://betpass20.com
Lose Belly Fat Learning On The Road-Trip With A Frustrated Chrissy Metz – Weightlosschallenge.
Weight Loss What Is So Great About The New Channel 4 Weight Loss Plan? – Weightlossjournal.
Lose Fat Chrissy Michaels Weight Loss Diet – Weightlosstracker.
Lose Weight Compare Metabolism Programs – Weightlossquotes.
Lose Belly Fat Oprah Winfrey Reveals Her Weight Loss Journey In Her Own Show – Weightlosshypnosis.
Diet A Review Of The Tv Show, €This Is Us†– Weightlossmotivation.
Weight Loss A Review Of The Thrill Of Chrissy Metz’ Weight Loss Journey | By ÖMer Gal | Jun, 2021 | Medium.
Lose Fat A Weight Loss Comparison Study Of Chrissy Michaels | By Meltem Tombul | Jun, 2021 | Medium.
Lose Belly Fat Revealing The Truth About Chrissy Metz Weight Loss Secret | By Kubra Aslä± | Jun, 2021 | Medium.
Lose Weight Personality Secrets €” Will €Œchrissy Metz Weight Loss†Get You Down? | By Aytekin Hos | Jun, 2021 | Medium.
Weight Lose A Realistic Book About Chrissy Michaels Weight Loss Diet | By Eråÿan ÖZcan | Jun, 2021 | Medium.
Forex margin trading information and recommendations. We will do our best to verify that we can introduce you to a site that you can trust and trust.
Weight Loss Inspirational Chrissy Metze Before And After Photos – Celine Dion Weight Loss.
Lose Weight Chrissy Metz’S Weight Loss Journey – Celine Dion Weight Loss.
Lose Fat Celine Dion Weight Loss Journey, Before And After [2021] – Our Daily Plus.
Lose Belly Fat Bestweightloss2022.
Lose Belly Fat The Weight Loss Plan 2022.
Lose Belly Fat Free Weightloss Method 2022.
Diet Plans For Weightloss 2022.
Weight Loss Weightnearmeloss.
Lose Weight Weight Loss Tips For Free ** 2022 **.
Lose Fat Celine Dion Weight Loss Reason And Health Issues – Celine Dion Weight Loss.
Diet Does Celine Dion Needed To Worry About Weight Loss Before And After A Challenge With The Abc News Team? – Celine Dion Weight Loss.
Diet Celine Dion Weight Loss Before And After Surgery – Celine Dion Weight Loss.
Lose Weight Stress And Weight Loss.
Lose Belly Fat Celine Dion Weight Loss Before And After – Celine Dion Weight Loss.
Diet Weightlossdetox.
Lose Belly Fat Weightlossgummies.
Lose Belly Fat Callweightloss.
Diet Adele Weightloss.
Lose Fat Alisonweightloss.
Lose Weight Weightlossmedium.
Weight Lose Site Title.
Lose Belly Fat Weight Loss Programs Near Me.
Healthy Diet Weight Loss Journey.
Lose Fat Vegan Diet Weight Loss.
Lose Fat Weightlosstransformation.
Diet Weightlosschallenge.
Weight Loss Weightlossjournal.
Weight Loss Weightlossquotes.
Weight Loss Weightlosshypnosis.
Weight Lose Weightlossmotivation.
Lose Weight Feeling Brainy? Test Your Smarts With This Weightloss Quiz.
Weight Loss The Intriguing Psychology Behind Weight Loss Diet.
Weight Loss Chumlee Weight Loss.
Diet Weight Loss Motivation Quotes.
Diet Weight Loss Affirmations.
Lose Belly Fat How To Quit Your Day Job And Focus On Weightloss.
Healthy Diet Weight Loss Injections.
Diet The Sick Truth Of Keto Diet.
Weight Loss Some Feel-Good News About Keto Diet To Brighten Your Day.
Lose Belly Fat 5 Unbelievable Things You Never Knew About Weightloss.
Lose Fat Best Healthful Meals Tips You Will Read This Year.
Healthy Diet Weight Loss Motivation.
Lose Fat If Ketogenic Is So Bad, Why Don’t Statistics Show It?.
Weight Lose Exercises Awards: 8 Reasons Why They Don'T Work &Amp; What You Can Do About It.
Diet Knowing These 5 Secrets Will Make Your Flat Belly Look Amazing.
Lose Belly Fat Motivation To Lose Weight.
Lose Belly Fat Imagine You Weightloss Tips Like An Expert. Follow These 10 Steps To Get There.
Lose Weight Easy Low Carb Food Recipes ** Low Carb Meals Easy ** Loss Weight Challenge &Amp; Weight Loss Det.
Lose Weight Easy Exercises To Lose Weight.
Lose Belly Fat 3 Months Weight Loss Diet.
Diet Best Pre Workout For Weight Loss.
Healthy Diet Best Laxatives For Weight Loss.
Diet Tops Weight Loss Program Ideas.
Lose Fat Weight Loss Running.
Lose Weight Slim And Sassy Weight Loss Program.
Diet Weight Loss 90 Days.
Lose Weight Weight Loss 90 Days.
Lose Weight Weight Loss 6 Weeks.
Lose Weight Weight Loss Running.
Lose Weight Sara Haines Weight Loss.
Lose Fat How Much Weight Can You Lose In 3 Months.
Diet How Much Weight Can I Lose In 3 Months.
Healthy Diet How Long Does It Take To Lose Belly Fa.
Diet 32 Foods That Burn Belly Fat Fast.
Lose Fat How To Lose Belly Fat In 3 Days.
Weight Lose How To Lose 2 Pounds A Week.
Lose Fat How To Jump Start Weight Loss.
Thank you bro. Really good
Healthy Diet What To Eat For Weight Loss.
Diet What To Eat For Weight Loss.
Weight loss Best Weight Loss Program 2021.
Weight loss What To Eat For Weight Loss.
Hi, thanks for share.
Not only Tom but also Kevin went to the library.
Tom and Jenny went to the school.
Sarah cracked such a bad joke that no one laughed.
먹튀검증
Thank you for giving me great information https://hongmen.com.vn/san-pham/nha-bao-ve
Thank you for giving me great information bốt gác di động
Want to buy a mobile phone but don’t know which one should you buy? If you want so; then you are most welcome in this article because we are ready to give you the best possible information about the Vivo Mobile Price in BD. The most recent updated transportable value in BD, likewise as Vivo smartphone reviews in Bangladesh 2020. We tend to give the foremost engaging mobile news publisher in Bangladesh in 2020 an agency unfold mobile news in a sense. Try to be with us for getting lots of valuable information about the Vivo Mobile Price in Bangladesh. In our beloved site, we have gathered all the information about the Vivo mobile price.
We dismembered everything on this site basically the best Knowledge, Best Vivo Mobile Price in Bangladesh of the models that you wouldn’t find on some other site. You can without a genuinely stunning stretch eccent
Update Information
This site will give every one of you the latest updates that are related to PDAs. We made each model out of different brands in such a manner, that will help you in separating one model and another.
Runner two Bike is and a few-wheeled engine vehicle. There are three essential sorts of cruisers: road, rough terrain, and double reason. Inside these sports, there are many sub-sorts of bicycles for exceptional purposes. There is consistently a dashing partner to each kind. Every setup presents both a particular increase or tremendous ability, and every design makes an uncommon utilizing stance.
Runner Bicycle Gifts or Inconveniences
RUNNER two is among the most professional producers of bicycles and they serve a worldwide market conveying close by Runner Bike Price in BD an enormous variety of contraptions going from fine models. A part of the experts Samsung phones has incorporated the going with.
OnePlus become once the most significant phone organization inside the world. How times change. In 2020 however it’s considering a to be as a financial limit to mid-go Android player, with two or three premium handsets tossed certain great measure.
OnePlus Points of Interest and Downsides
OnePlus is among the chief genius creators of phones which they serve an overall commercial center conveying close by OnePlus Mobile Price in BD a broad assortment of devices
Thanks for reading. That is a great observation. In fact, a student wrote on her test that she had difficulty figuring out when to use product rule versus chain rule.Çankaya Tesisatçı 7/24 su tesisat plumber hizmet.
I appreciate, cause I found just what I was looking for. You have ended my four day long hunt! God Bless you man. Have a great day. Bye
토토사이트
카지노사이트
Thanks for sharing excellent informations. Your web-site is very cool. I’m impressed by the details that you have on this site. It reveals how nicely you understand this subject. Bookmarked this web page, will come back for more articles. You, my pal, ROCK! I found simply the information I already searched all over the place and simply couldn’t come across. What a great web-site.
Useful information. Lucky me I found your web site by chance, and I’m shocked
why this coincidence did not took place earlier! I bookmarked it.
파워볼사이트닷컴
Really nice and interesting post. I was looking for this kind of information and enjoyed reading this one.
Watch in real-time of cryptocurrency prices, Bitcoin
Price (BTC) , ethereum, litecoin and altcoins from major cryptocurrency exchanges…
FIFO Calculator, first in-first out, means the items that were bought first are the first items sold.
Ending inventory is valued by the cost of items most recently purchased. First-In,
First-Out method can be applied in both the periodic inventory system and the perpetual inventory system.
I think it will be more complete if you add some topics to this article. I have these types of articles on my blog
Very informative blog, This blog is very easy to understand when compared to other blogs.
There is clearly a great deal to think about this. I think you made some great focuses in Features too.
This is one very interesting post. I like the way you write and I will bookmark your blog to my favorites. 온라인홀덤
Calculus is very hard problem
اقتصاد آفرین، سامانه جامع تحلیل اخبار اقتصادی
I have this site recommendation for you, Just follow the given link here:
What’s up, the whole thing is going nicely here and ofcourse every one is sharing information, that’s actually good, keep up writing.
I’ve stayed on your blog quite a long time. There was so much to do. Please write a lot of funny stories in the future.
Such an amazing and helpful post this is. I really really love it. It’s so good and so awesome.
Great article, This post helps me a lot Thank you. Anyways I have this site recommendation for you, Just follow the given link here
Wow, Very nice post it’s all information is really helpful for all users. Thanks for sharing and I am waiting for your next post.
It’s very informative and you are obviously very knowledgeable content on your site. You have opened my eyes to varying views on this topic with interesting and solid content, thanks for sharing
I am really impressed by reading the information content you provided. It is very unique and useful. I really appreciate the time and effort you spend to share this with us! I do hope to read more updates from you.
I’m still learning from you, but I’m making my way to the top as well. I absolutely enjoy reading everything that is posted on your website.Keep the aarticles coming. I liked it!
The article composing business is going extraordinary for me at this moment, and the vast majority of my prosperity is because of the substance that you post here. I utilize your substance to compose my articles, and the substance makes my great article incredible. 온라인포커
That is really fascinating, You’re a very skilled blogger.
I’ve joined your rss feed and stay up for in search
of more of your excellent post. Additionally, I’ve shared your site
in my social networks
I’m not positive the place you’re getting your info, however good topic.
I needs to spend a while learning much more or understanding more.
Thank you for magnificent info I used to be looking for this info for my mission.
Wonderful article! We are linking to this particularly great content on our
website. Keep up the great writing.
Hi there, You have done a great job. I will definitely digg it and
personally recommend to my friends. I am confident they will be benefited from this web site.
Thanks for the info.
It’s really great. Thank you for providing a quality article. There is something you might be interested in. Do you know 온라인홀덤 ?
Great post! I am actually getting ready to across this information, is very helpful my friend. Also great blog here with all of the valuable information you have. Keep up the good work you are doing here. 온라인포커
My brother suggested I may like this blog. He used to be totally right.
This post actually made my day. You can not believe
simply how much time I had spent for this information! Thank you! 온라인경마
It as really a great and helpful piece of info. I am glad that you shared this helpful info with us. Please keep us up to date like this. Thank you for sharing. 토토
Very good article, Its really great blog thank you for sharing important information!
Can you win big on online casinos? 실시간바카라 ❤️
Amazing knowledge and I like to share this kind of information with my friends and hope they like it they why I do.
Just about all I can express is, I don’t know what to say! Except naturally, for the amazing tips which are shared using this blog.
I like material like this. This is a great article and I really enjoyed reading it. You have an original style that makes your ideas stand out from other writers.
turkish #emekserverler, #emek pvp serverler, #metin2 pvp serverler, #emek serverler, #metin2 thenks admin http://www.emekserverler.net
Pretty! This was an extremely wonderful post. Thank you for providing this info 배트맨토토
THE ON http://wslikserverler.net GAMES
Thenks admin aradıgınız tum metin2 pvp serverler,i bu sitede yani http://editsizserverler.org adresinde bulabilrisiniz, editsiz serverler için en guzel adres
Fitter, happier,düz okey more productive, duz okey comfortable,not drinking too much, regular exercise at the gym(3 days a week),getting on better with your associate duz okey oyna employee contemporaries https://duzokeyoynaa.com
I think this is one of the most important information for me. And I am happy to read your article. Thanks for sharing! 정선바카라 ❤️
Engaging in oral sex is a great workout to reduce calories, as in the 26 minutes you go you burn the calories of one pizza. During fetalization, the nerve roots of the lips are irritated and oxytocin is released, which allows the woman to relax. https://onlineokeyoynaa.com
Hello, I’ve been working with the target db for over 5 years with the work team.
We will always try to profit from sales and marketing with the latest DB. 디비
If you contact us anytime 24 hours a day, we will be kindly consulted.
Hello, I’ve been working with the target db for over 5 years with the work team.
We will always try to profit from sales and marketing with the latest DB. 디비
If you contact us anytime 24 hours a day, we will be kindly consulted.
This is such a comprehensive resource that you are presenting and you give it away for free. I am hoping the same best work from you in the future as well. Thanks for sharing this informative information with us. Take a look at my blog …온라인바카라 It’s my pleasure to see you there!
Some really quality posts on this website , saved to favorites .
situs resmi permainan kartu Online terpercaya
Thankfulness to my father who shared with me
on the topic of this blog, this website is in fact awesome. Try this site too and explore at this site. 라이브카지노 . ?
I would also motivate just about every person to save this web page for any favorite assistance to assist posted the appearance.
thank you so much
Everything is very open with a precise description of the challenges. Keep posting such kind of information. It was definitely informative. Your site is extremely helpful. Thank you for sharing!
If you have a time feel free to visit my webpage: 인터넷카지노 It’s my pleasure too see you there!
I really saw your site back I are regularly glancing through which dependably. You have a heaps of data at this website so I genuinely like your look to the web a piece too. Keep up the best show results!
I actually saw your site back I are normally looking through which reliably. You have a stacks of information at this site so I truly like your look to the web a piece also. Keep up the best show results!
Hi to all, the contents present at this site are actually amazing for people experience, well, keep up the nice work fellows.Feel free to visit my blog post..
Goodd site you’ve got here.. It?s difficult to finnd good quality writing like yours these days. I seriously appreciate peoplle like you! Take care!!my blog
This is my first time pay a visit at here and i am in fact pleassant to read all at single place.
Your email address is never share
The winning formula relies in part on taking Western hit shows and marketing or adapting them for a different audience. In 2019, it launched a special season of “Queer Eye”, where the cast performed makeovers in Japan. In December, it announced a South Korean version of “Money Heist,” a Spanish crime drama that has received critical acclaim and from the public.
I’m eager to uncover this page. I need to thank you for ones time for this especially phenomenal read!! I unquestionably truly loved all aspects of it and I additionally have you saved to fav to take a gander at new data in your site
tratamento alcoolismo
tratamento dependencia quimica
clinica de reabilitação
clinica de recuperação
agencia de marketing digital em São Paulo SP, desenvolvemos todo marketing digital para sua empresa, SEO, Links Patrocinados, Mídias
agencia de marketing digital
Really informative and inoperative, Thanks for the post and effort! Please keep sharing more such blog .
I would also motivate just about every person to save this web page for any favorite assistance to assist posted the appearance.
hayatta başaramadığım şeylerden biridi matematik ve fiziktir
Amazing knowledge and I like to share this kind of information with my friends and hope they like it they why I do.
It’s consistently a delight to peruse your heavenly articles on this site. You are among the top essayists of this age, and there’s nothing you can do that will change my assessment on that. My companions will before long acknowledge how great you are.
Thank you for sharing! You write interesting posts as for me. But if you want to post it on instagram, you need to get many followers. Read this blog post to know how to get insta followers https://socialnewsdaily.com/89226/social-media-influencer-trends-2020/
Great site!
Thanks
The syllabus covered limits and derivatives. Among other problems, I always ask students to write down the derivative formulas and then give an assortment of derivative problems. Here is the relevant segment of the test:
I regularly visit this site to check out the events and functions and sometimes for resources. However, it has been a while that you have shared some news about latest or upcoming events.
I’ve read your article, and I think it very useful. thanks for sharing 🙂
Travel Agent Medan
Regardless of what the student’s needs are, they can find support through online paper help services. This will guarantee that they do well in school and their instructive improvement will progress at a movement that they are skilled to deal with.
I always ask students to write down the derivative formulas and then give an assortment of derivative problems. Here is the relevant segment of the test:
Good
Here is the relevant segment of the test:
Betcup canlı bahis sitesi
Restbet bahis sitesi
Amazing knowledge and I like to share this kind of information with my friends and hope they like it they why I do.
thank you your article very help me, your article highly recommended once.
genel forum
I like viewing web sites which comprehend the price of delivering the excellent useful resource free of charge. I truly adored reading your posting. Thank you!
In my experience what is most critical in students being able to be successful in doing problems like those in 5
OKEY salonu, okey oyunu, okey oyna, real okey, canlı okey oyna, online okey oyna, bedava okey oyna, okey, Okey salonları, okey siteleri, okey sitesi
experiment several times to draw a meaningful conclusion. Still, there may be completely unexpected lurking variables.
Not that correlation implies causation or anything, just that there is one.
encontrado las condiciones óptimas para campar a sus anchas y provocar una epidemia, dejando tras de si un rastro de enfermos y bursa cty
https://betpas.life
It is good test! But it is easy for me
Such lovely… Bravo!
You really did a great work here… Kudos
figurin e chain rul
encontrado las condiciones óptimas para campar a sus anchas y provocar una epidemia, dejando tras de si un rastro de enfermos y bursa cty https://bursaokey.com bursa cty colapsando los servicios de urgencias de los hospitales
encontrado las condiciones óptimas para campar a sus anchas y provocar una epidemia, dejando tras de si un rastro de enfermos y bursa cty https://bursaokey.com bursa cty colapsando los servicios de urgencias de los hospitales.
fisting gay porn make porn avatar amy reid on porn hub babysitters forced anal
Thanks for sharing this awesome post. Its a nice place to visit.
izmir okey
I know this site offers quality dependent articles or reviews and additional stuff,
is there any other site which presents such things in quality? Jim Michael
This is a wonderful blog, this is very informative for me. Thanks for sharing it…
Much appreciated such a great amount with this phenomenal new site. I’m extremely started up to show it to anybody. It makes me so fulfilled your tremendous comprehension and insight have another channel for attempting into the world
I’m eager to reveal this page. I have to thank you for ones time for this especially awesome read!! I unquestionably truly enjoyed all aspects of it and I likewise have you spared to fav to take a gander at new data in your site
It is also just that I realized the weakness of my website. konveksi tas
https://karyabintangabadi.com often has problems in dealing with the analysis problem. But may I ask about this analysis
sometimes I still think about the test analysis problem of the law. it’s very hard to learn if you can help me on https://pabriktasmurah.id
waw, this analysis requires a special instruction in its development.
i think its same with https://sentrakonveksitas.com
This was helpful i appreciate
We provide our services to clients located anywhere in the world. The internet is a great tool that enables us to help any
company regardless of its location.
Hey I am so captivated I discovered your blog, I really discovered you unintentionally, while I was watching on google for something else, Anyways I am here now and could just like to state thank for a gigantic post and an all around connecting with webpage. Mercifully keep up the exceptional work.
More than a site, we are building a successful and redid propelled procedure.
We urge, we support, we co-pilot …
Our main responsibility is to gain a result as per your objectives.
blois-tribu-and-co.fr
nice one here
nice write-up here
However, to answer the question more accurately I would have to give another class a test and allow them to have a formula sheet. Then I could compare the test scores of the two classes to see if one class did significantly better than the other. And what if one class just happens to have stronger students than the other? Then I would have to repeat the experiment several times to draw a meaningful conclusion. Still, there may be completely
cunymathblog.commons.gc.cuny.edu/2013/04/08/analysis-of-a-calculus-test-part-i/
I really love this post!!!
Thanks for the share but, Download Free African Mp3 and Latest Songs from Top South African, Nigerian, Ghanaian and East African Artists. Stream and download high quality mp3 and listen to popular playlists.
jeniuspoker merupakan daftar situs idn poker online terbaik tahun 2020 karena berhasil mempertahankan keamanan dan kenyamanan bermain kepada membernya sejak idn poker versi lama loh..
Jangan ketinggalan meraih bonus seumur hidup dan hadiah global jackpot yang turun setiap harinya. Pendaftaran akun baru gratis tanpa di pungut biaya!!
Web resmi –> http://162.0.225.20/~jeniuspoker/
l in students being able to be successful in doing problems like those in 5. is that they are comfortable with the pattern recognition skills (parsing the question if you like) so they can te
Am a fan of your site, keep it up
This article really helped thanks web admin
Perfect piece of work i appreciate your works
Am a fan of your site, keep it up
To facilitate the revision of the contents in the following sections we will see (Glaser & Straus, The discovery of grounded theory: strategies for qualitative research., 1967):
up wearing a suit jacket and carry a wallet.” “Some people have a clear idea of what they would like to be, but this is not enough, because identity requires social validation”
I noticed a correlation (0.72) between knowing the derivative formulas and finding the derivatives of more complicated functions correctly. Not that correlation implies causation or anything, just that there is one.
great post
I love this
Your story-telling style is witty, keep up the good work!
Very great post
Thanks for this article, it really clarify a lot of things
Wow i did not think i can find it easy like this, thank so much
Download Latest 2020 Foreign HipHop music, HipHop news, HipHop video, HipHop Album & Eps , Mp3 Download on Yahiphop.com
Download Latest South Africa Songs, videos, album & eps For Free mp3 Download Read News
I can now understand
sich besonders Lammfell oder das Fell ist ausgesprochen soft und zur gleichen Zeit schonend für das
bietet sich besonders oder das Fell ist ausgesprochen soft und zur gleichen Zeit schonend für das Pferd.
Jetzt bietet sich besonders Lammfell Der Stoff oder das Fell ist ausgesprochen soft und zur gleichen Zeit schonend für das Pferd.
Jetzt bietet sich besonders Lammfell an. Der Stoff oder das Fell ist ausgesprochen soft und zur gleichen Zeit schonend für das Pferd.
correlation is 0.56, which is less, but still notable.
Would you say knowing formulas is predictive of solving derivative problems correctly on a test? Most calculus instructors would agr
I noticed a correlation (0.72) between knowing the derivative formulas and finding the derivatives of more complicated functions correctly. Not that correlation implies causation or anything, just that there is one.
o in my Calculus I class. The syllabus covered limits and derivatives. Among other problems, I always ask students to write down the derivative formulas and then give an assortment of d
online okey oyunu http://okey-net.com
USA popiler online okey games https://realokey.com
ks ago in my Calculus I class. The syllabus covered limits and derivatives. Among other problems, I always ask students to write down the derivative formulas and then give an assortment of deri
latest nasty c songs download
ne class did significantly better than the other. And what if one class just happens to have stronger students than the other? Then I would have to
ne class did significantly better than the other. And what if one class just happens to have stronger students than the other? Then I would have to
this with this light before. This article truly did switch topic goes http://bandarxl.xyz/
nice post.. i will learn latter..
poker trosss
please come here and visit http://w88messi.biz/
great post you have guys and i really like it.. please visit us at http://jampoker.co
good post and lovely
I like it and i will share it to others. Join us at http://bolanet88.biz
thanks
please join with us soon
http://ratugol.com
Thanks for sharing this nice post. just follow http://lagapoker.net
you have a great post and i like it.. please join us at http://goopoker.com
good post
One of the great and useful post, i really like it. Thanks for sharing this nice post. Great efforts made here keep the efforts up and thanks for the efforts. visit http://pokernet88.co
thank you your article very help me, your article highly recommended once
While this subject can be very touchy for most people, my opinion is that there has to be a middle or common ground that we all can find. I do appreciate that you’ve added relevant and intelligent commentary here though. Thanks!
Pingback: Analysis of a Calculus Test – Part 2 | CUNYMath Blog
Thanks for reading. That is a great observation. In fact, a student wrote on her test that she had difficulty figuring out when to use product rule versus chain rule. I will add a segment to my homeworks and tests to address this explicitly.
In my experience what is most critical in students being able to be successful in doing problems like those in 5. is that they are comfortable with the pattern recognition skills (parsing the question if you like) so they can tell if they will need the product rule, the quotient rule, the chain rule in its “full glory,” just the power rule version of the chain rule (as is the case for 5b), or a mixture of these rules.